Introduction to Hypothesis Testing

Overview

Teaching: 45 min
Exercises: 10 min

Questions

• What are inferential statistics?

• What is a hypothesis?

• How can I test a hypothesis?

Objectives

• Define a null and alternative hypothesis

• Understand the hypothesis-testing process

• Recognise the different types of hypothesis testing errors

Hypothesis Testing

The following is a well-established research pipeline:

1. Define a research question, or hypothesis
2. Design an appropriate study or trial to test that hypothesis
3. Conduct the study or trial
4. Observe, collate and process the results (data)
5. Measure the agreement with the hypothesis
6. Draw conclusions regarding the hypothesis

In this model, the hypothesis should be clearly defined and testable. In hypothesis testing, this means that our question has just two possible answers: a ”null hypothesis” (H₀), which is a specific statement that we are looking to disprove with our data, and an “alternative hypothesis” (H₁), which is a statement opposing H₀ and which we will only accept if the data and analysis is sufficiently convincing.

Tip: Defining your alternative hypothesis

The alternative hypothesis must cover all options not included in the null hypothesis; if H₀ is: “There is no difference between A and B”, then H₁ must be: “A and B are different”, not: “A is greater than B”. Generally, a two-sided test (“A and B are different”) is regarded as better practice than a one-sided test (“A is greater than B”).

Challenge 1

Imagine you were testing a new medical treatment. What might be the most appropriate null and alternative hypotheses?

1. Null – the new treatment is worse than the existing treatment. Alternative – the new treatment is better than the existing treatment
2. Null – there is no difference between the new and old treatments. Alternative – there is a difference between the new and existing treatments
3. Null – there is a difference between the new and existing treatments. Alternative – there is no difference between the new and existing treatments
4. Null – there is no difference between the new and old treatments. Alternative – the new treatment is better than the existing treatment

Solution to challenge 1

Option 2 is the correct answer - the default assumption (the null hypothesis) is that there is no difference between the two treatments, and we need convincing evidence to accept that the new treatment has a different outcome (the alternative hypothesis). Think about why the other options may not be suitable. Can you come up with another valid null and alternative hypothesis?

When carrying out hypothesis testing, we normally use a standard framework.

1. We establish our null and alternative hypothesis
2. We collect data, often by measurement or experimentation on a small sample group representative of the whole population
3. From the data, we calculate a test statistic – an estimation of a population parameter derived from the data – and a rejection region – a range of values for the test statistic for which we would reject H₀ and accept H₁
4. If the test statistic falls within the rejection region and we accept H₁, we can calculate a p-value, the probability of the observed test statistic (or one more favourable to H₁) occurring if H₀ were true.

Hypothesis testing is often used in inferential statistics, where measurements are taken on a random sample from a large population in order to estimate (or infer) something about that population as a whole. Example of inferential statistics include opinion polls and drug trials.

Challenge 2

Would results from a population census be an example of inferential statistics? If you are in a face to face class, you might like to discuss this with your neighbour.

Solution to challenge 2

Probably not, because a census is an attempt to directly measure the whole population, not just a representative sample. However there is nearly always some missing data and inference may be used in an attempt to compensate for that.

p-values and rejection of the null hypothesis

• The null hypothesis is tested against the alternative one using a distribution of a statistic.
• The p-value is the probability of obtaining results as extreme as the observed results of a statistical hypothesis test, assuming that the null hypothesis is correct.
• The probability of rejecting H₀, given the truth of H₀, is called the significance level, denoted α (often α=0.05, but as low as α=0.0000003 in some disciplines)
• The significance level, denoted α, is the probability of rejecting H₀ when H₀ is true. For instance, a significance level of 0.05 indicates there is a 5% risk of incorrectly concluding a difference exists when there is no actual difference (often α=0.05, but can be as low as α=0.0000003 in some disciplines).
• If the p-value < 0.05, we are 95% confident when we reject H₀
  • Conclusion: we can reject H₀

Confidence intervals

A confidence interval gives more information than the results of a hypothesis test (reject or don’t reject): it provides a range of plausible values for the parameter being studied. Example: If the sample mean is used to estimate the population mean, the confidence interval gives the upper and lower bounds of a range in which we have 95% confidence that the real population mean occurs.

Challenge 3

What conclusion can you make if your analysis gives a p-value of 0.994?

1. You can accept the alternative hypothesis with high confidence
2. You can accept the alternative hypothesis with low confidence
3. There is insufficient evidence to reject the null hypothesis
4. You can neither accept nor reject the alternative hypothesis

Solution to challenge 3

Option 3. If the p-value is above our chosen significance level (commonly 0.05, 0.01 or 0.001) we don’t have sufficient evidence to reject the null hypothesis. Note - this does not necessarily mean that the null hypothesis is true, rather that we have don’t have adequate justification to conclude otherwise.

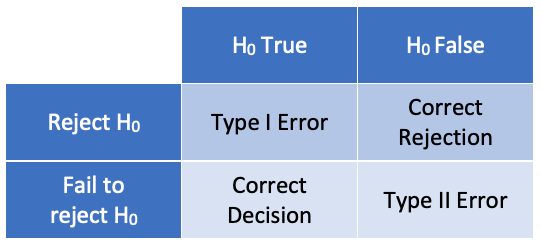
Testing errors

In hypothesis testing, there are two possible causes for a false conclusion: rejecting the null hypothesis when it is true (a type I error), or failing to reject the null hypothesis when it is false (a type II error). The probability of a type 1 error is given by the p-value; it is possible to calculate the probability of a type II error, but we will not cover that in this course.

Key Points

• Select appropriate and testable null and alternative hypotheses

• Interpret p-values and statistical significance correctly