Data Preparation
Overview
Teaching: 45 min
Exercises: 30 minQuestions
What data will we be using?
How do I load the data?
Objectives
Introduction to RStudio
Loading the data
Introduction to RStudio
We will be using RStudio throughout this workshop, and so the first prerequisite is installing R and RStudio. Upon installing and opening RStudio, you will be greeted by three panels:
- The interactive R console/Terminal (entire left)
- Environment/History/Connections (tabbed in upper right)
- Files/Plots/Packages/Help/Viewer (tabbed in lower right)
Opening a text file (such as an R or Rmd file) in RStudio will open the file in a new panel in the top left.
There are two main ways that you can run R commands or scripts within RStudio:
- The interactive R console
- This works well when running individual lines to test code and when starting your analysis.
- It can become laborious and inefficient and is not suitable when running many commands at once.
- Writing in a .R / .Rmd file
- All of your code is saved for editing and later use.
- You can run as many lines as you wish at once.
The hash symbol (#) can be used to signal text in our script file that should not be run, which are called comments. An example of using comments to describe code is shown below.
# Chunk of code that will add two numbers together
1 + 2 # Adds one and two together
Tip: Running segments of code
There are a few ways you can run lines of code from a .R file. If you want to run a single line, place your cursor at the end of the line. If you want to run multiple lines, select the lines you would like to run. We have a few options for running the code:
- click on the Run button above the editor panel, or
- hit Ctrl+Return (⌘+Return also works if you are using OS X)
If you are using a .R file and edit a segment of code after running it and want to quickly re-run the segment, you can press the button to the right of the Run button above the editor panel to re-run the previous code region.
Tip: Getting help in R
For help with any function in R, put a question mark before the function name to determine what arguments to use, some examples and other background information. For example, running
? histwill give you a description for base R’s function to generate a histogram.If you don’t know the name of the function you want, you can use two question marks (??) to search for functions relating to a keyword (e.g.
?? histogram)
First Example - Data Dictionary
Today, we will be working on two data sets throughout the day to understand correlation and linear regression in R.
In our first example we will use a data set consisting of 100 individuals with 13 different measurements taken. This is data of medical records, vitals and clinical examinations of participants with heart disease. Descriptions of the 13 variables are given in the data dictionary below.
| Variable | Description |
|---|---|
| Age | Age in years |
| Sex | Sex; 0=Female, 1=Male |
| Cp | Chest Pain; 1=Typical Angina, 2=Atypical Angina, 3=Non-Anginal pain, 4=Asymptomatic |
| Trestbps | Resting Systolic BP in mmHg |
| Chol | Blood Cholesterol Level in mg/dl |
| Fbs | Fasting Blood Sugar; 0 = less than 120mg/dl and 1= greater than 120 mg/dl |
| Exang | Exercise Induced Angina; 0=No, 1=Yes |
| Thalach | Maximum Heart Rate Achieved |
| Old Peak ST | ST wave depression induced by exercise |
| Slope | The slope of peak exercise segment; 1=Up-sloping, 2=Flat, 3=Down Sloping |
| Ca | Number of major vessels coloured by fluoroscopy |
| Class | Diagnosis Class; 0=No disease, 1-4 Various stage of disease in ascending order |
| restecg | Resting ECG abnormalities; 0=Normal, 1=ST Abnormality, 2=LVH |
Working Directory
The working directory is a file path on your computer that is the default location of any files you read or save in R. You can set this directory Files pane in RStudio, as shown below.
You can also set the working directory in the menu bar, under Session -> Set Working Directory.
Alternatively, you can do this through the RStudio console using the command setwd by entering the absolute filepath as a string.
Use getwd to get the current working directory.
For example, to set the working directory to the downloads folder on Mac or Windows, use
setwd("~/Downloads") # for Mac
setwd("C:\Users\YourUserName\Downloads") # for Windows
Importing and Preparing the Data
First, import the data into your R environment as a data frame and display its dimensions.
heart <- read.csv("data/heart_disease.csv")
dim(heart)
## [1] 100 14
From this we know that we have 100 rows (observations) and 14 columns (variables): 1 identification variable and 13 measurement variables.
Tip: stringsAsFactors
When importing data with columns containing character strings to be used as categories (e.g. male/female or low/medium/high), we can set the
stringsAsFactorsargument asTRUEto automatically set these columns to factors.
We can use the str function to look at the first few observations for each variable.
str(heart)
## 'data.frame': 100 obs. of 14 variables:
## $ ID : int 1 2 3 4 5 6 7 8 9 10 ...
## $ age : int 63 67 67 37 41 56 62 57 63 53 ...
## $ sex : int 1 1 1 1 0 1 0 0 1 1 ...
## $ chol : int 233 286 229 250 204 236 268 354 254 203 ...
## $ fbs : int 1 0 0 0 0 0 0 0 0 1 ...
## $ thalach : int 150 108 129 187 172 178 160 163 147 155 ...
## $ trestbps: int 145 160 120 130 130 120 140 120 130 140 ...
## $ restecg : int 2 2 2 0 2 0 2 0 2 2 ...
## $ exang : int 0 1 1 0 0 0 0 1 0 1 ...
## $ oldpeak : num 2.3 1.5 2.6 3.5 1.4 0.8 3.6 0.6 1.4 3.1 ...
## $ slope : int 3 2 2 3 1 1 3 1 2 3 ...
## $ ca : int 0 3 2 0 0 0 2 0 1 0 ...
## $ class : int 0 2 1 0 0 0 3 0 2 1 ...
## $ cp : int 1 4 4 3 2 2 4 4 4 4 ...
Using the summary function, we can view some information about each variable.
summary(heart)
## ID age sex chol fbs
## Min. : 1.00 Min. :37.00 Min. :0.00 Min. :141.0 Min. :0.00
## 1st Qu.: 25.75 1st Qu.:48.75 1st Qu.:0.00 1st Qu.:215.2 1st Qu.:0.00
## Median : 50.50 Median :55.50 Median :1.00 Median :239.0 Median :0.00
## Mean : 50.50 Mean :54.73 Mean :0.71 Mean :246.5 Mean :0.13
## 3rd Qu.: 75.25 3rd Qu.:60.25 3rd Qu.:1.00 3rd Qu.:270.8 3rd Qu.:0.00
## Max. :100.00 Max. :71.00 Max. :1.00 Max. :417.0 Max. :1.00
## thalach trestbps restecg exang oldpeak
## Min. : 99.0 Min. :104.0 Min. :0.00 Min. :0.0 Min. :0.000
## 1st Qu.:142.0 1st Qu.:120.0 1st Qu.:0.00 1st Qu.:0.0 1st Qu.:0.400
## Median :155.5 Median :130.0 Median :2.00 Median :0.0 Median :1.000
## Mean :152.2 Mean :133.2 Mean :1.14 Mean :0.3 Mean :1.235
## 3rd Qu.:165.8 3rd Qu.:140.0 3rd Qu.:2.00 3rd Qu.:1.0 3rd Qu.:1.800
## Max. :188.0 Max. :180.0 Max. :2.00 Max. :1.0 Max. :6.200
## slope ca class cp
## Min. :1.00 Min. :0.00 Min. :0.00 Min. :1.00
## 1st Qu.:1.00 1st Qu.:0.00 1st Qu.:0.00 1st Qu.:3.00
## Median :1.50 Median :0.00 Median :0.00 Median :3.00
## Mean :1.61 Mean :0.59 Mean :0.85 Mean :3.18
## 3rd Qu.:2.00 3rd Qu.:1.00 3rd Qu.:1.00 3rd Qu.:4.00
## Max. :3.00 Max. :3.00 Max. :4.00 Max. :4.00
Recoding Variables
Looking at the summary output, we can see that the categorical variables such as sex, slope and class are being treated as numerical data. We can fix this by setting these categorical variables as factors.
To do this, we can use as.factor on each of the categorical columns in our data frame, specifying the levels and labels of each variable as arguments.
heart$ID <- as.factor(heart$ID)
heart$sex <- factor(heart$sex,levels = c(0, 1), labels = c("Female", "Male"))
heart$fbs <- factor(heart$fbs,levels = c(0, 1), labels = c("<120", ">120"))
heart$restecg <- factor(heart$restecg,levels = c(0, 1, 2), labels = c("Normal", "ST Abnormality", "LVH"))
heart$exang <- factor(heart$exang,levels = c(0, 1), labels = c("No", "Yes"))
heart$slope <- factor(heart$slope,levels = c(1, 2, 3), labels = c("Up-sloping", "Flat", "Down-sloping"))
heart$cp <- factor(heart$cp,levels = c(1, 2, 3, 4), labels = c("Typical angina", "Atypical angina", "Non-Anginal pain", "Asymptomatic"))
For the class variable, we will merge the four levels of disease into a single “disease” factor, leaving us with a binary variable.
heart$class <- as.factor(heart$class)
levels(heart$class)[which(levels(heart$class) == "0")] <- "No Disease"
levels(heart$class)[which(levels(heart$class) %in% c("1", "2", "3", "4"))] <- "Disease"
Running summary on the data again, now with the correct types, will give us the correct description of the data (counts for categorical variables and a five number summary and mean for the numerical variables).
summary(heart)
## ID age sex chol fbs
## 1 : 1 Min. :37.00 Female:29 Min. :141.0 <120:87
## 2 : 1 1st Qu.:48.75 Male :71 1st Qu.:215.2 >120:13
## 3 : 1 Median :55.50 Median :239.0
## 4 : 1 Mean :54.73 Mean :246.5
## 5 : 1 3rd Qu.:60.25 3rd Qu.:270.8
## 6 : 1 Max. :71.00 Max. :417.0
## (Other):94
## thalach trestbps restecg exang oldpeak
## Min. : 99.0 Min. :104.0 Normal :43 No :70 Min. :0.000
## 1st Qu.:142.0 1st Qu.:120.0 ST Abnormality: 0 Yes:30 1st Qu.:0.400
## Median :155.5 Median :130.0 LVH :57 Median :1.000
## Mean :152.2 Mean :133.2 Mean :1.235
## 3rd Qu.:165.8 3rd Qu.:140.0 3rd Qu.:1.800
## Max. :188.0 Max. :180.0 Max. :6.200
##
## slope ca class cp
## Up-sloping :50 Min. :0.00 No Disease:57 Typical angina : 7
## Flat :39 1st Qu.:0.00 Disease :43 Atypical angina :13
## Down-sloping:11 Median :0.00 Non-Anginal pain:35
## Mean :0.59 Asymptomatic :45
## 3rd Qu.:1.00
## Max. :3.00
##
We can now use this data in our analyses!
Key Points
Make sure you set your working directory.
View a summary of your data to ensure your variables are of the right type.
Correlation
Overview
Teaching: 45 min
Exercises: 45 minQuestions
How can we tell if two variables are correlated?
What test(s) do we use to test for correlation?
Objectives
Test the correlation between a number of variables in our data set.
Learn how to determine which test to use, depending on the types of the variables.
Introduction
Correlation describes the degree of association between two variables and is most commonly used to measure the extent to which two variables are linearly related.
Associations can be positive, where an increase in one variable is associated with an increase in the other, or negative, where an increase in one variable is associated with a decrease in the other.
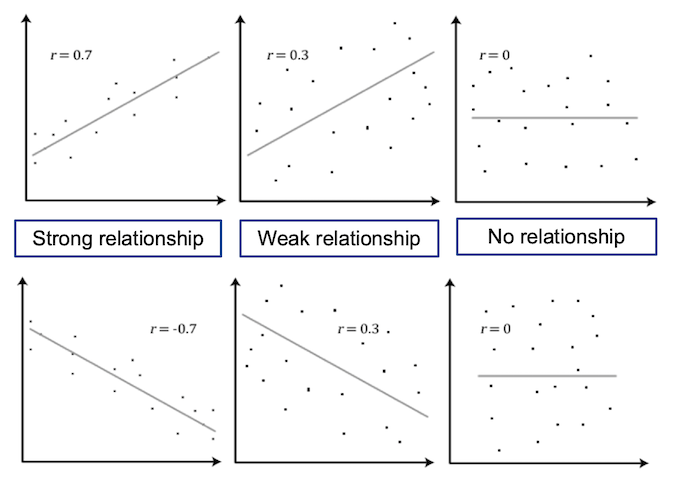
Challenge 1
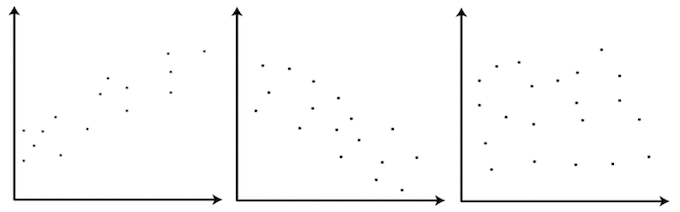
Label the following three scatter plots as showing no correlation or a positive or negative correlation
Solution to Challenge 1
- Left image: Positive correlation
- Middle image: Negative correlation
- Right image: No correlation
There are different tests for measuring correlation, depending on the distribution of those variables:
- Pearson’s correlation coefficient: Used for the correlation between two continuous and normally distributed variables
- Spearman’s rank test: Used for the correlation between two continuous variables where at least one is non-normally distributed
- Kendall’s Tau: Used for the correlation between two ordinal (non-continuous) variables.
Correlation R Functions
Two R functions for measuring and testing the significance of association are cor and cor.test, where the correlation coefficient to be computed can be specified as an argument to the function (either “pearson” (default), “spearman”, “kendall”). cor simply computes the correlation coefficient, while cor.test also computes the statistical significance of the computed correlation coefficient.
Pearson’s Correlation Coefficient
The Pearson’s correlation coefficient (r) is defined as
[r = \frac{\sum_i (x_i - \bar x)(y_i - \bar y)}{\sqrt{\sum_i (x_i - \bar x)^2(y_i - \bar y)^2}}]
and varies between -1 and 1, where 1 indicates a perfect positive linear relationship and -1 indicates a perfect negative linear relationship. Here, \(\bar{x}\) is the mean of all values of \(x\).
A common interpretation of the value of r is described in the table below
| Value of r | Relationship |
|---|---|
| |r| = 0 | No relationship |
| |r| = 1 | Perfect linear relationship |
| |r| < 0.3 | Weak relationship |
| 0.3 ≤ |r| ≤ 0.7 | Moderate relationship |
| |r| = 0.7 | Strong relationship |
Coefficient of Determination
Pearson’s \(r\) can be squared to give us \(r^2\), the coefficient of determination, which indicates the proportion of variability in one of the variables that can be accounted for by the variability in the second variable.
For example, the if two variables X and Y have a Pearson’s correlation coefficient of r = -0.7, then the coefficient of determination is \(r^2\) = 0.49. Thus, 49% of the variability in variable X is determined by the variability of variable Y.
Visualising Relationships
Scatter plots are useful for displaying the relationship between two numerical variables, where each point on the plot represents the value of the two variables for a single observation. This is useful in the exploratory phase of data analysis to visually determine if a linear relationship is present.
The figure below shows a scatter plot of variables with different levels of correlation.
Exercise - Correlation Analysis
For the first exercise we will test for correlation between age and resting systolic blood pressure. The steps for conducting correlation are:
- Testing for normality: before performing a correlation test, we will look at normality of variables to decide if we are going to use a parametric or non parametric test.
- Choosing and performing the correct test.
- Interpreting the analysis results.
Testing for Normality
Normality can be tested by:
- Visualising the data through a histogram, and
- Conducting Shapiro-Wilk’s test.
We can produce a histogram for a numerical variable using the hist function.
hist(heart$trestbps)
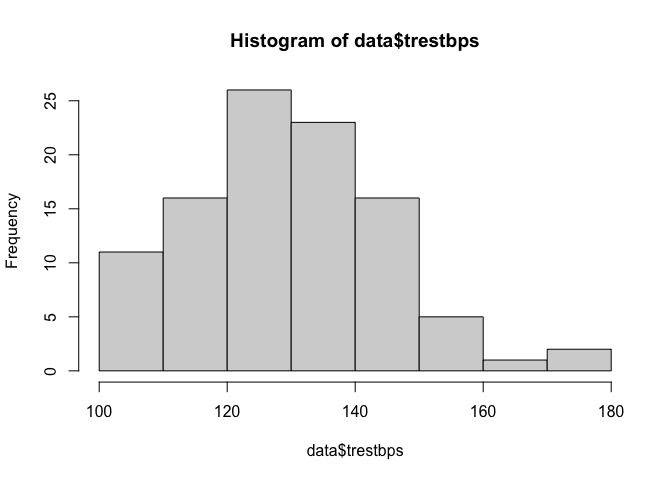
It appears that the variable could potentially be normally distributed, although slightly skewed, but we should analytically test this assumption.
We can perform a Shapiro-Wilk normality test for this variable using the shapiro.test function.
shapiro.test(heart$trestbps)
##
## Shapiro-Wilk normality test
##
## data: heart$trestbps
## W = 0.96928, p-value = 0.01947
The null hypothesis of the Shapiro-Wilk normality test is that the data comes from a normal distribution. The p-value resulting from this test is significant and so we can reject the null hypothesis that the data is normally distributed and infer that it is not normally distributed.
Selecting and Performing the Correct Test
Because our data is continuous but not normally distributed, we will estimate the correlation between SBP and age using a
non-parametric test: Spearman’s rank test. The correlation between SBP and age can be estimated using the cor function. Here,
we round the result to 2 decimal places and assign it to the correlation variable to be used later.
correlation <- round(cor(heart$trestbps, heart$age, method = "spearman"), 2)
Further, we can test the significance of this finding using the cor.test function.
cor.test(heart$trestbps, heart$age, method = "spearman")
##
## Spearman's rank correlation rho
##
## data: heart$trestbps and heart$age
## S = 121895, p-value = 0.0069
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## 0.2685589
Interpreting the Analysis Results
The null hypothesis for this test is that there is no correlation (rho = 0), and the alternative hypothesis is that there is a correlation (rho is not equal to 0). The resulting p-value for this test is 0.0069, and therefore there is significant evidence that there is moderate correlation between Age and resting SBP level.
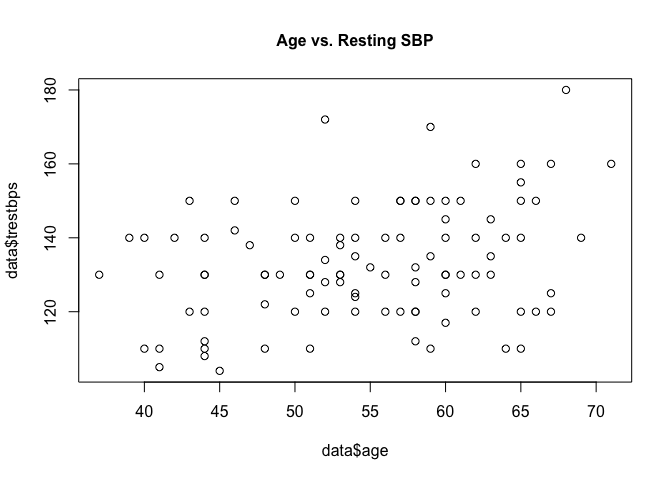
Plotting age and resting SBP on a scatter plot can help us visually understand the association.
plot(heart$trestbps ~ heart$age, main = "Age vs. Resting SBP", cex.main = 1)
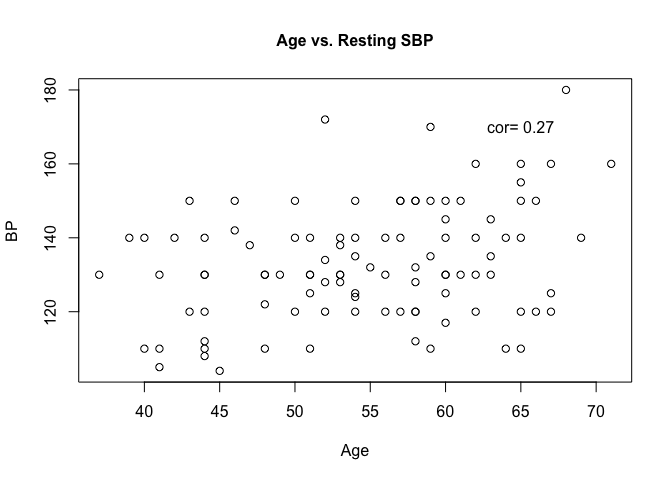
Additional arguments can be given to the plot function to customise the look and labels of the plot.
plot(heart$trestbps ~ heart$age,
main = "Age vs. Resting SBP",
cex.main = 1,
cex.lab = 1,
xlab = "Age",
ylab = "BP",
cex = 1,
pch = 1)
text(x = 65,
y = 170,
label = paste("cor = ", correlation))
The arguments we supplied to the plot function are
- main: Main title
- xlab: X axis label
- ylab: Y axis label
- cex: How much the text (titles, axis labels etc.) should be scaled relative to the default (1).
- cex.main: Scaling factor of the main title relative to cex
- cex.lab: Scaling factor of the axis labels relative to cex
- pch: Number representing the symbol to be used (list symbols available in the R docs).
We also used the text function to insert the correlation value we computed earlier into the image.
ggplot2 is a popular data visualisation package that offers an elegant framework for creating plots. We can use geom_point to create a scatter plot and geom_smooth to add a linear least squares regression line to the data.
library(ggplot2)
ggplot(heart, aes(x = age, y = trestbps)) +
geom_point(shape = 1) +
geom_smooth(method = lm, se = F)+
ggtitle("Age vs.Resting BP")
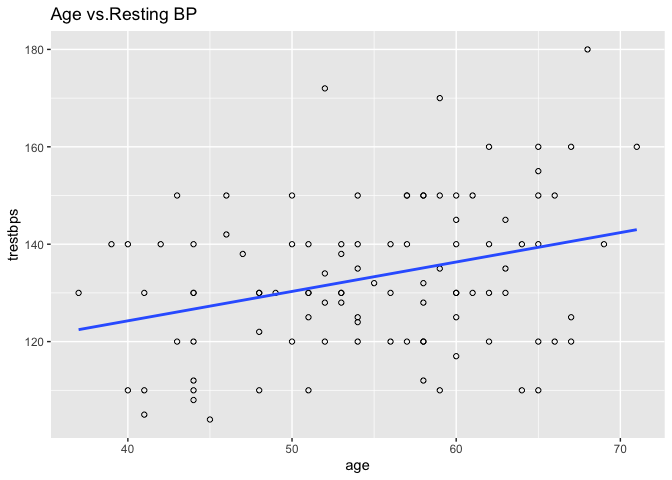
Calling ggplot2() initialises a ggplot object.
We use this to declare the data frame that contains the data we want to visualise as well as a plot aesthetic (aes).
A plot aesthetic is a mapping between a visual cue and a variable.
In our example, we specify that age is to be on the x-axis and resting SBP on the y-axis.
The specified plot aesthetic will be used in all subsequent layers unless specifically overridden.
We then add geom_point and geom_smooth layers to the plot, as well as a title layer.
Exploring Relationship Between SBP and Other Continuous Variables
Challenge 2
- Plot the relationship between SBP and Cholesterol on a scatter plot.
- Test for a correlation between these two variables; can we be confident in this estimate?
- Do the results of the test and the plot agree?
Solution to Challenge 2
To plot the data, we use the plot function.
plot(heart$trestbps ~ heart$chol, main = "Cholesterol vs. Resting SBP", cex.main = 1)The plot appears to show a positive correlation, although very weak. A test should be performed to confirm this finding. As we are confident SBP is not normally distributed, we will use Spearman’s rank to determine the correlation.
cor.test(heart$trestbps, heart$chol, method = "spearman")This shows we have a weak positive correlation, and the p-value suggests we are confident in this statement.
Instead of running an individual test for each variable, we can test for multiple at a time by indexing the relevant columns of
the heart data frame.
However, we will first separately analyse the ‘ca’ variable, the number of major vessels coloured by fluoroscopy, as this is an ordinal variable, which requires we use Kendall’s Tau to measure correlation.
round(cor(heart$trestbps, heart$ca, method = "kendall"), 2)
## [1] -0.05
cor.test(heart$trestbps, heart$ca, method = "kendall")
##
## Kendall's rank correlation tau
##
## data: heart$trestbps and heart$ca
## z = -0.5971, p-value = 0.5504
## alternative hypothesis: true tau is not equal to 0
## sample estimates:
## tau
## -0.04876231
We can obtain a vector indexing the numeric variables in our dataset using a combination of functions in a single line. We will exclude the 12th column as this is the ‘ca’ column.
mydata <- heart[-c(12)]
cont <- as.vector(which(sapply(mydata, is.numeric)))
Let’s break this one-liner down:
is.numeric(x) returns TRUE if the input x is a numerical value, such as 2 or 62.14, and FALSE for all other types, such as factors or strings.
sapply(list, function) applies the function argument to each item in the list argument.
So, sapply(heart, is.numeric) will return a list of TRUE or FALSE denoting whether each column (or variable) of our data is numeric.
which(x) returns a list of the TRUE indices in a logical vector (a vector of only TRUE or FALSE).
So the result of our one-liner above will be a vector containing the column numbers of the variables that our numerical in our data set.
We can grab the data under each of these variables using our cont vector and test the correlation of each our numeric variables with BPS using Pearson’s correlation coefficient.
round(cor(mydata$trestbps, mydata[, cont], method = "spearman", use = "pairwise.complete.obs"), 2)
## age chol thalach trestbps oldpeak
## [1,] 0.27 0.21 -0.07 1 0.2
The correlation between BPS and BPS is 1, as this “relationship” is completely linear.
We can visualise the correlation between each pair of variables using ggcor, from the GGally package.
myvars <- c("trestbps", "age", "chol", "thalach", "oldpeak")
newdata <- heart[myvars]
library(GGally)
ggcorr(newdata, palette = "RdBu", label = TRUE)
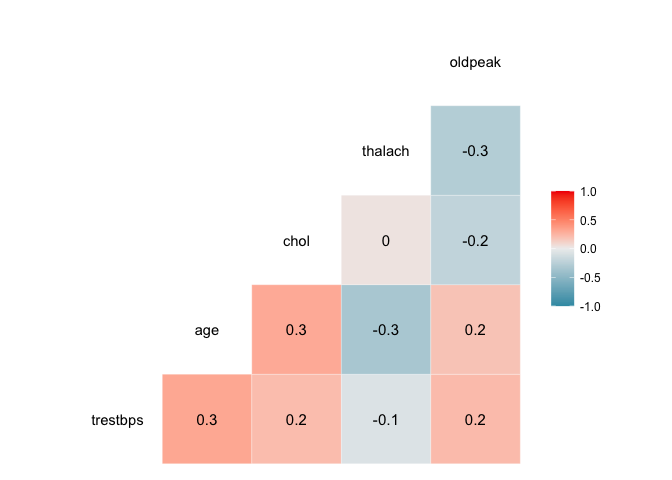
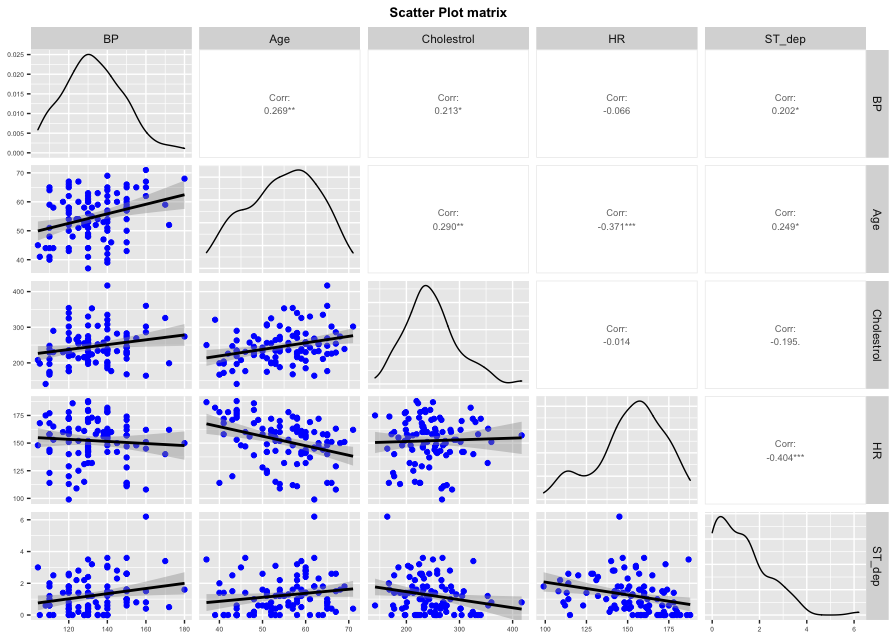
ggpairs plots a scatter plot with the correlation for each pair of variables; it also plots an estimated distribution for each variable.
ggpairs(newdata, columns = 1:5, columnLabels = c("BP", "Age", "Cholestrol", "HR", "ST_dep"),
lower = list(continuous = wrap( "smooth", colour = "blue")), upper = list(continuous = wrap("cor", method = "spearman", size = 2.5))) +
ggtitle("Scatter Plot matrix") +
theme(axis.text = element_text(size = 5),
axis.title = element_text(size = 5),
plot.title = element_text(size = 10, face = "bold", hjust = 0.5))
Key Points
There are different tests to test for correlation, depending on the type of variable.
Plots are useful to determine if there is a relationship, but this should be tested analytically.
Use helpful packages to visualise relationships.
Simple Linear Regression
Overview
Teaching: 60 min
Exercises: 60 minQuestions
What is linear regression?
What are the assumptions we need to meet to use linear regression?
How do I perform linear regression in R?
How do I ensure that my data meets the model assumptions?
Objectives
Understand theory of linear regression.
Use linear regression on our dataset.
Check the model diagnostics to ensure the data meets the assumptions of linear regression.
Regression analysis is used to describe the relationship between a single dependent variable \(Y\) (also called the outcome) and one or more independent variables \(X_1, X_2, \dots, X_p\) (also called the predictors). The case of one independent variable, i.e. \(p = 1\), is known as simple regression and the case where \(p>1\) is known as multiple regression.
Simple Linear Regression
In simple linear regression, the aim is to predict the dependent variable \(Y\) based on a given value of the independent variable \(X\) using a linear relationship. This relationship is described by the following equation: \(Y = a + bX + e\)
where \(a\) is the intercept (the value of \(Y\) when \(X = 0\)) and \(b\) is the regression coefficient (the slope of the line). \(e\) represents an additive residual term (error) that accounts for random statistical noise or the effect of unobserved independent variables not included in the model.
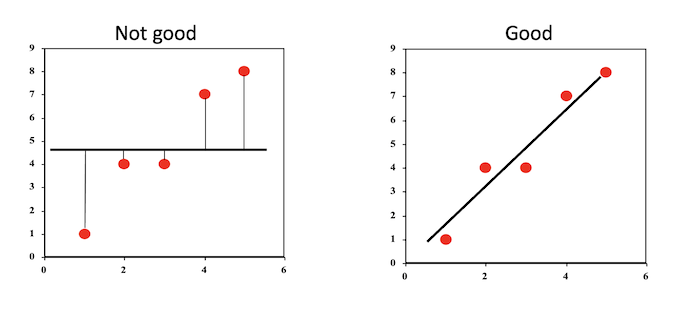
In simple linear regression, we wish to find the values of a and b that best describe the relationship given by the data.
This objective can be thought of as drawing a straight line that best fits the plotted data points.The line can then be used to predict Y from X.
Least Squares Estimation
Ordinary least squares (OLS) is a common method used to determine values of a and b through minimising the sum of the squares of the residuals, which can be described mathematically as the problem \(\min_{a, b} \sum_i (Y_i - (a + bX_i))^2\)
Solving through calculus, the solution to this problem is \(\hat{b} = \frac{\sum_i (x_i - \bar x) (y_i - \bar y)}{\sum_i (x_i - \bar x)^2}\) and \(\hat{a} = \bar y - \hat{b} \bar x\) .
In the figure below, we have four observations and two lines attempting to fit the data.
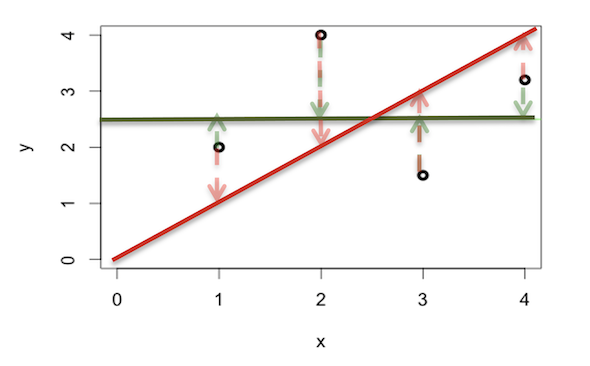
The sum of squares for the red sloped line is \((2 - 1)^2 + (4 - 2)^2 + (1.5 - 3)^2 + (3.2 - 4)^2 = 7.89\) and the sum of squares for the green flat line is \((2 - 2.5)^2 + (4 - 2.5)^2 + (1.5 - 2.5)^2 + (3.2 - 2.5)^2 = 3.99\)
As the sum of squares for the green line is smaller, we can say it is a better fit to the data.
The coefficient \(b\) is related to the correlation coefficient \(r\) where \(r = b\frac{\text{SD}_X}{\text{SD}_Y}\). If \(X\) and \(Y\) are positively correlated, then the slope \(b\) is positive.
Regression Hypothesis Test
We can estimate the most suitable values for our model, but how can we be confident that we have indeed found a significant linear relationship? We can perform a hypothesis test that asks: Is the slope significantly different from 0?
Hypothesis
- \(H_0: b = 0\) (no linear relationship)
- \(H_1: b \neq 0\) (linear relationship)
Test of Significance: \(T = \hat{b}\ / \text{SE}(\hat{b})\)
Result: p-value significant or not
Conclusion: If p-value is significant, then the slope is different from 0 and there is a significant linear relationship.
Standard Error
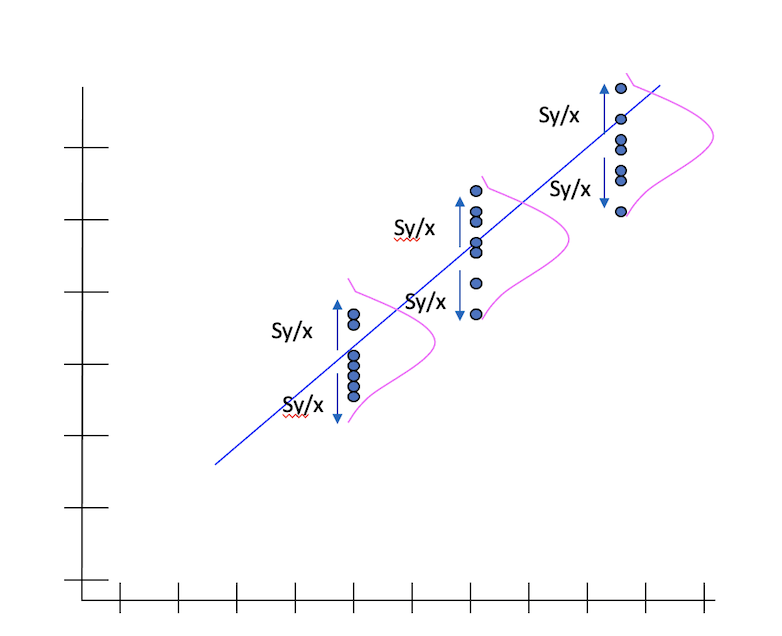
The standard error of Y given X is the average variability around the regression line at any given value of X. It is assumed to be equal at all values of X. Each observed residual can be thought of as an estimate of the actual unknown “true error” term.
Assumptions of Linear Regression
There are four assumptions associated with using linear models:
- The relationship between the independent and dependent variables is linear.
- The observations are independent.
- The variance of the residuals is constant across the observations (homoscedasticity).
- The residuals are normally distributed with mean 0.
These assumptions can be considered criteria that should be met before drawing inferences from the fitted model or using it to make predictions.
The residual \(e_i\) of the \(i\)th observation is the difference between the observed dependent variable value \(Y_i\) and the predicted value for the value of the independent variable(s) \(X_i\): \(e_i = Y_i - \hat{Y}_i = Y_i - (a + bX_i)\)
Coefficient of Determination
The coefficient of determination \(R^2\) represents the proportion of the total sample variability (sum of squares) explained by the regression model. This can also be interpreted as the proportion of the variance of the dependent variable that is explained by the independent variable(s). The most general definition of the coefficient of determination is \(R^2 = 1 - \frac{SS_{res}}{SS_{tot}}\) where \(SS_{res}\) is the sum of the squares of the residuals as defined above and \(SS_{tot}\) is the total sum of squares \(SS_{tot} = \sum_i (Y_i - \bar Y)^2,\) which is proportional to the variance of the dependent variable.
Example - Cigarettes and Coronary Heart Disease
Example from Landwehr & Watkins (1987) and cited in Howell (2004).
Let us consider the following research question: How fast does CHD mortality rise depending on smoking?
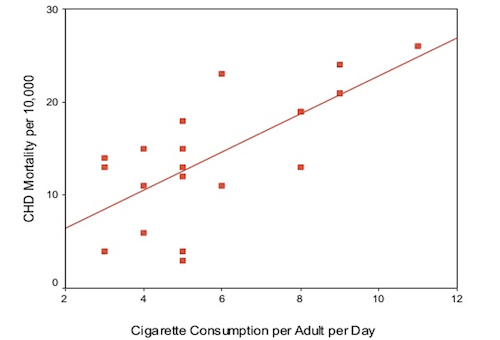
This can be framed as a linear regression problem, where each observation is a particular country and the independent variable is the average number of cigarettes smoked per adult per day and the dependent variable is the CHD mortality rate (deaths per 10,000 per year due to CHD). The data we will use in this example is given in the table below and visualised in the scatter plot, with a line of best fit, below:
| Cig. | CHD |
|---|---|
| 11 | 26 |
| 9 | 21 |
| 9 | 24 |
| 9 | 21 |
| 8 | 19 |
| 8 | 13 |
| 8 | 19 |
| 6 | 11 |
| 6 | 23 |
| 5 | 15 |
| 5 | 13 |
| 5 | 4 |
| 5 | 18 |
| 5 | 12 |
| 5 | 3 |
| 4 | 11 |
| 4 | 15 |
| 4 | 6 |
| 3 | 13 |
| 3 | 4 |
| 3 | 14 |
As a reminder, the linear regression equation is \(\hat Y = a + bX.\)
In this example, \(Y\) is the CHD mortality rate (CHD) and \(X\) is the average number of cigarettes smoked per adult per day (CigCons), so the equation is \(\text{CHD}_{\text{pred}} = a + b \times \text{CigsCons} + e.\)
The intercept \(a\) represents the predicted CHD mortality rate in a nation where the average number of cigarettes smoked per adult per day is zero. The slope \(b\) represents the rate of increase of CHD mortality rate for each unit increase in the average number of cigarettes smoked per adult per day.
Regression Results
The results of fitting a linear model to the data is shown below.

The p-value associated with the prediction of the slope is less than 0.05, indicating there is significant evidence that the slope is different from zero, and therefore there is a significant relationship between cigarette consumption and CHD mortality.
Substituting these values into our linear regression equation, we get the predicted model:
[\text{CHD}_{\text{pred}} = 2.37 + 2.04 \times \text{CigsCons}]
We can interpret this as:
- CHD mortality is equal to 2.37 on average when 0 cigarettes are consumed;
- CHD mortality increases by an average of 2.04 units per unit increase in cigarette consumption.
Making a Prediction
We may want to predict CHD mortality when cigarette consumption is 6, which can be done using our model.
[\text{CHD}_{\text{pred}} = 2.37 + 2.04 \times 6 = 14.61]
and so we predict that on average 14.61/10,000 people will die of CHD per annum in a country with an average cigarette consumption of 6 per person per day.
Residuals
Now that we have a fitted model, we can check the residuals between our model and the data we used to fit the model. In simple regression, the residuals is the vertical distance between the actual and predicted values for each observation; an example of the residual for a particular observation is shown in the figure below.
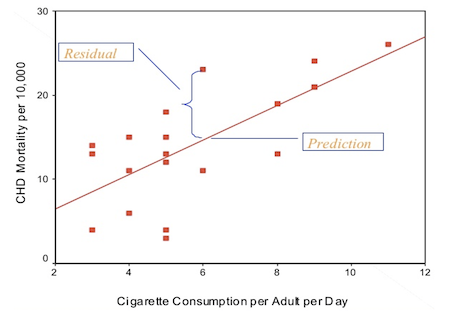
For one observation, there was a CHD mortality of 23 deaths per 10,000 with the average number of cigarettes smoked per adult per day is 6. Our prediction for the same cigarette consumption level was 14.61 deaths per 10,000, and so the residual for this observation is 23 - 14.61 = 8.39.
For this model, we obtained an \(R\) value of 0.71. Squaring this, we get \(R^2\) = 0.51, and so we find that almost 50% of the variability of incidence of CHD mortality is associated with variability in smoking rates.
Linear Regression R Functions
result <- lm(Y ~ X, data = data): Get estimated parameters of regressionsummary(result): Display results of linear regressionconfint(result): Get confidence intervals around estimated coefficientsfitted(result): Get predicted values for Yresid(result: Get the residuals of the model
Exercise - SBP and Age
In this exercise we will be exploring the relationship between systolic blood pressure (the dependent variable) and age (the independent variable) using linear models.
First, we will use a scatter plot to visually check that there is a linear relationship.
plot(heart$trestbps ~ heart$age)
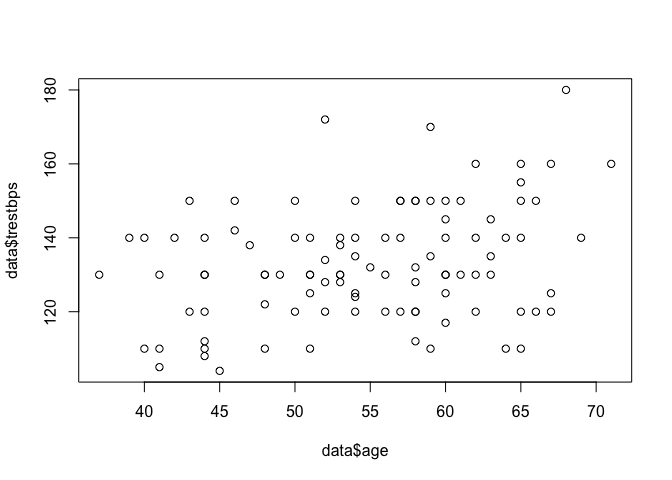
The lm function is used to fit a linear model and obtain the estimated values of $a$ and $b$, and we can use the summary function to view a summary of the results.
model1 <- lm(trestbps ~ age, data = heart)
summary(model1)
##
## Call:
## lm(formula = trestbps ~ age, data = heart)
##
## Residuals:
## Min 1Q Median 3Q Max
## -29.362 -11.385 -0.823 10.185 40.489
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 100.1066 10.1527 9.860 2.44e-16 ***
## age 0.6039 0.1835 3.291 0.00139 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 14.83 on 98 degrees of freedom
## Multiple R-squared: 0.09951, Adjusted R-squared: 0.09033
## F-statistic: 10.83 on 1 and 98 DF, p-value: 0.001389
Under the Coefficients heading, we can view information about the predicted variables and their significance. We see that age has a significant effect on SBP (p = 0.00139) and for each year increase in age there is a 0.60 unit increase in SBP level.
The confint function gives us a 95% confidence interval for each model parameter estimate.
confint(model1)
## 2.5 % 97.5 %
## (Intercept) 79.9588567 120.2542931
## age 0.2397537 0.9681186
We can interpret the 95% confidence interval for the relationship with age as: We can be 95% confident that the range 0.24 to 0.97 contains the true value of the linear relationship between age and SBP.
The coefficients function gives us the model coefficients, as outputted by summary.
coefficients(model1)
## (Intercept) age
## 100.1065749 0.6039361
fitted gives us the predicted SBP values for each value of age in our data set.
fitted(model1)
## 1 2 3 4 5 6 7 8
## 138.1546 140.5703 140.5703 122.4522 124.8680 133.9270 137.5506 134.5309
## 9 10 11 12 13 14 15 16
## 138.1546 132.1152 134.5309 133.9270 133.9270 126.6798 131.5113 134.5309
## 17 18 19 20 21 22 23 24
## 129.0955 132.7191 129.0955 129.6994 138.7585 135.1349 135.1349 135.1349
## 25 26 27 28 29 30 31 32
## 136.3427 130.3034 135.1349 139.9664 126.0758 124.2640 141.7782 136.3427
## 33 34 35 36 37 38 39 40
## 138.7585 135.7388 126.6798 125.4719 126.0758 134.5309 133.3231 136.9467
## 41 42 43 44 45 46 47 48
## 139.3624 124.2640 142.9860 135.7388 136.9467 135.1349 130.9073 130.3034
## 49 50 51 52 53 54 55 56
## 139.3624 132.1152 124.8680 139.3624 126.6798 126.6798 136.3427 132.7191
## 57 58 59 60 61 62 63 64
## 130.3034 124.8680 132.7191 130.9073 130.9073 127.8876 135.1349 132.7191
## 65 66 67 68 69 70 71 72
## 132.7191 136.3427 136.3427 132.7191 135.7388 127.8876 139.3624 140.5703
## 73 74 75 76 77 78 79 80
## 137.5506 139.3624 126.6798 139.3624 136.3427 130.9073 129.0955 135.1349
## 81 82 83 84 85 86 87 88
## 127.2837 132.1152 123.6601 141.1742 131.5113 126.6798 128.4916 132.1152
## 89 90 91 92 93 94 95 96
## 132.1152 130.9073 139.9664 137.5506 137.5506 126.6798 138.1546 131.5113
## 97 98 99 100
## 135.7388 136.3427 131.5113 129.0955
resid gives the residuals for each observation in our data set.
resid(model1)
## 1 2 3 4 5 6
## 6.8454481 19.4297035 -20.5702965 7.5477878 5.1320432 -13.9269989
## 7 8 9 10 11 12
## 2.4493842 -14.5309350 -8.1545519 7.8848095 5.4690650 6.0730011
## 13 14 15 16 17 18
## -3.9269989 -6.6797652 40.4887457 15.4690650 -19.0955098 7.2808734
## 19 20 21 22 23 24
## 0.9044902 0.3005541 -28.7584880 14.8651288 -15.1348712 -3.1348712
## 25 26 27 28 29 30
## -6.3427435 -10.3033820 -15.1348712 10.0336397 23.9241710 -14.2640206
## 31 32 33 34 35 36
## -1.7781688 -19.3427435 1.2415120 -0.7388073 3.3202348 14.5281071
## 37 38 39 40 41 42
## -6.0758290 15.4690650 -1.3230628 13.0533204 10.6375758 15.7359794
## 43 44 45 46 47 48
## 17.0139590 14.2611927 -6.9466796 -23.1348712 -20.9073182 19.6966180
## 49 50 51 52 53 54
## 0.6375758 -2.1151905 -19.8679568 -19.3624242 -14.6797652 3.3202348
## 55 56 57 58 59 60
## -6.3427435 -8.7191266 9.6966180 -14.8679568 -7.7191266 -5.9073182
## 61 62 63 64 65 66
## -0.9073182 14.1123625 -7.1348712 2.2808734 -12.7191266 8.6572565
## 67 68 69 70 71 72
## 3.6572565 17.2808734 34.2611927 22.1123625 15.6375758 -15.5702965
## 73 74 75 76 77 78
## -17.5506158 -29.3624242 -16.6797652 20.6375758 -11.3427435 9.0926818
## 79 80 81 82 83 84
## 0.9044902 14.8651288 -23.2837013 -2.1151905 16.3399155 38.8257674
## 85 86 87 88 89 90
## -11.5112543 13.3202348 9.5084264 -4.1151905 5.8848095 -0.9073182
## 91 92 93 94 95 96
## -19.9663603 22.4493842 -7.5506158 -18.6797652 -3.1545519 -3.5112543
## 97 98 99 100
## -25.7388073 13.6572565 2.4887457 -7.0955098
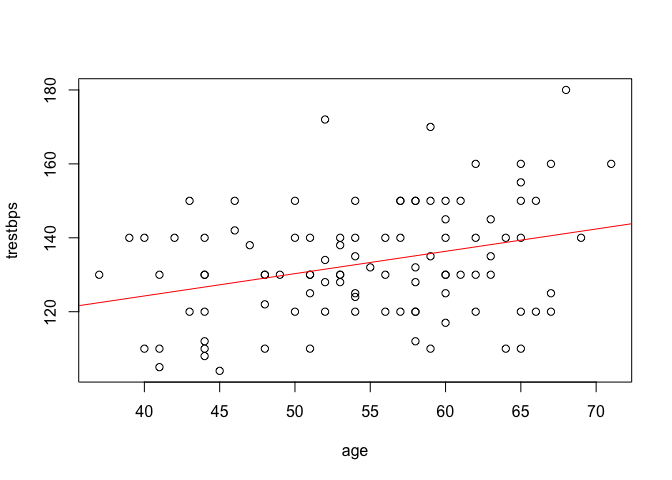
By using abline with our model after plotting a scatter plot, we can plot the estimated regression line over our data.
plot(trestbps ~ age, data = heart)
abline(model1, col = "red")
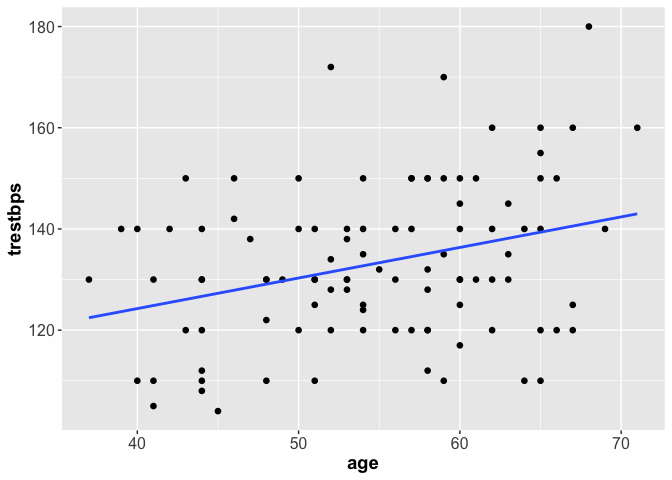
We can do the same with ggplot2.
library(ggplot2)
ggplot(heart, aes(x = age, y = trestbps)) +
geom_point(shape = 16, size = 2) +
geom_smooth(method = lm, se = F)+
theme(axis.text = element_text(size = 12),
axis.title = element_text(size = 14, face = "bold"))
Confidence and Prediction
We can use the predict function to predict SBP for each value of age in our data set and also get confidence or prediction intervals for each observation.
The type of interval is specified using the int argument to the function, with int = "c" for confidence intervals and int = "p" for prediction intervals.
Confidence intervals tell us how well we have determined the estimate parameters. The standard error for a CI takes into account the uncertainty due to sampling.
Prediction intervals tell us in what range a future individual observation will fall. The standard error for a PI takes into account the uncertainty due to sampling as well as the variability of the individuals around the predicted mean.
Both intervals will be centered around the same value but the standard errors will be different. A prediction interval is always wider than a confidence interval.
For example, here we obtain the confidence intervals for each prediction.
predict(model1, int = "c")
## fit lwr upr
## 1 138.1546 133.9440 142.3651
## 2 140.5703 135.2200 145.9206
## 3 140.5703 135.2200 145.9206
## 4 122.4522 115.3564 129.5480
## 5 124.8680 119.0662 130.6697
## 6 133.9270 130.9485 136.9055
## 7 137.5506 133.5924 141.5088
## 8 134.5309 131.4746 137.5872
## 9 138.1546 133.9440 142.3651
## 10 132.1152 129.1061 135.1243
...
Note that when we have a model fitted using lm, the predict and fitted functions give the same predicted values.
What can go wrong?
As discussed, there are some assumptions that need to be met to use a linear model and we must check if they are being violated before using our model to draw inferences or make predictions. Such violations are:
- In the linear regression model:
- Non-linearity (e.g. a quadratic relation or higher order terms).
- In the residual assumptions:
- Non-normal distribution;
- Non-constant variances;
- Dependency;
- Outliers.
The checks we need to make are:
- Linearity between outcome and predictors
- Plot residuals vs. predictor variable (if non-linearity try higher-order terms in that variable)
- Constant variance of residuals
- Plot residuals vs. fitted values (if variance increases with the response, apply a transformation to the data)
- Normality of residuals
- Plot residuals Q-Q norm plot (significant deviation from a straight line indicates non-normality)
Making the Checks
We can make the above checks manually by creating the necessary plots.
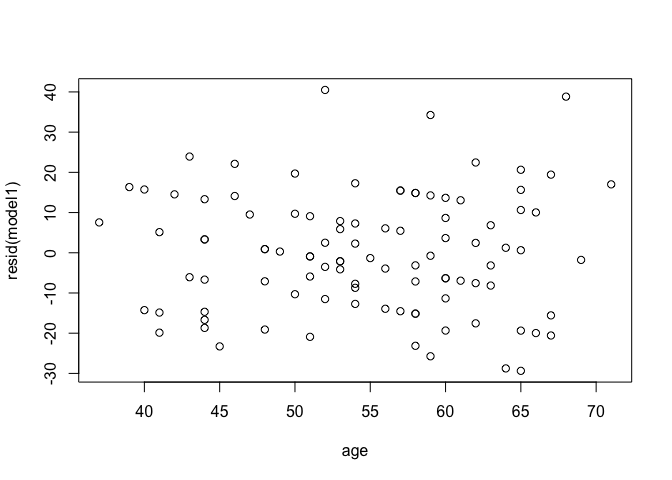
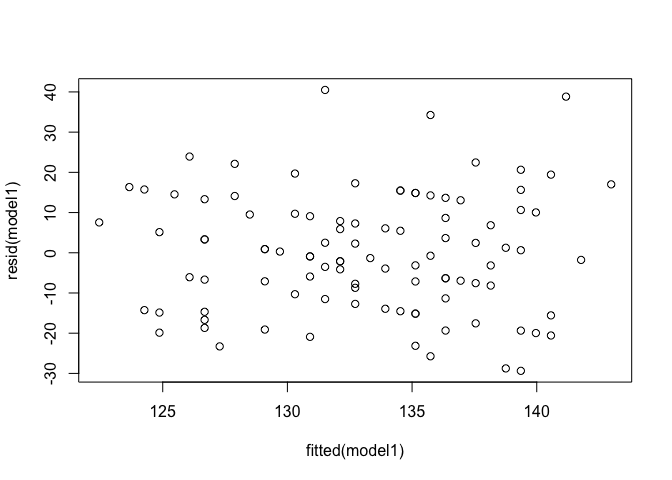
Linearity between outcome and predictor: Residuals vs predictor variable
plot(resid(model1) ~ age, data = heart)
Constant variance of residuals: Residuals vs fitted values
plot(resid(model1) ~ fitted(model1))
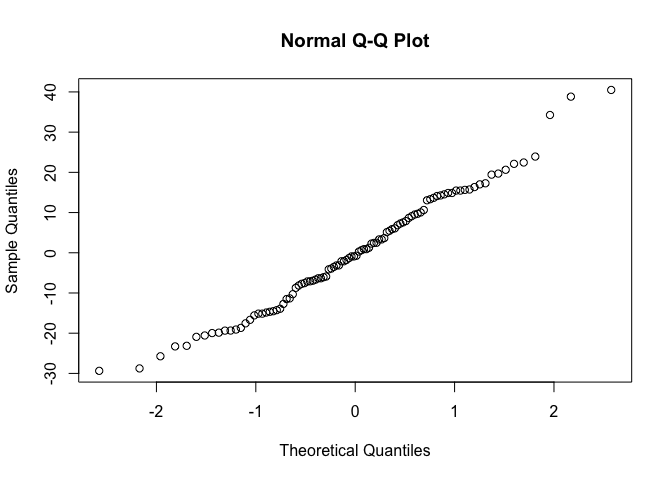
Normality of residuals: Q-Q plot of residuals
qqnorm(resid(model1))
Or, we can use R’s built-in diagnostic plotting with the plot function.
par(mfrow = c(2, 2))
plot(model1)
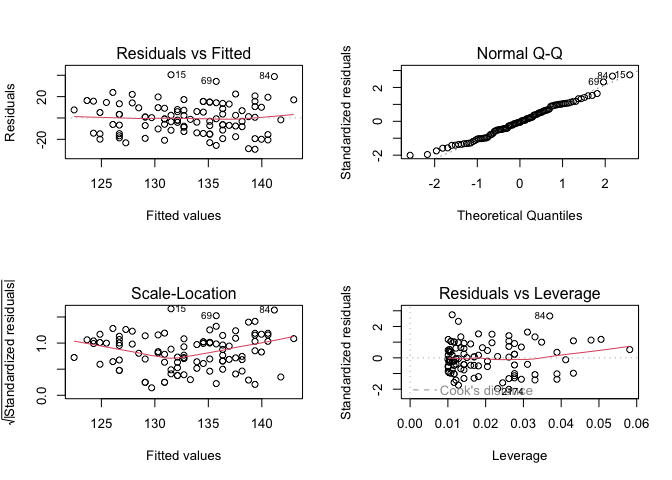
Let’s break down each of these plots.
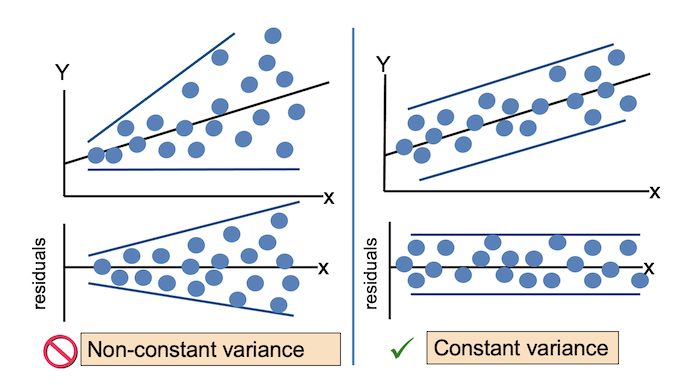
For the Residuals vs Fitted plot, the residuals should be randomly distributed around the horizontal line representing a residual error of zero; that is, there should not be a distinct trend in the distribution of points. Good and bad examples of these plots are shown in the figures below.
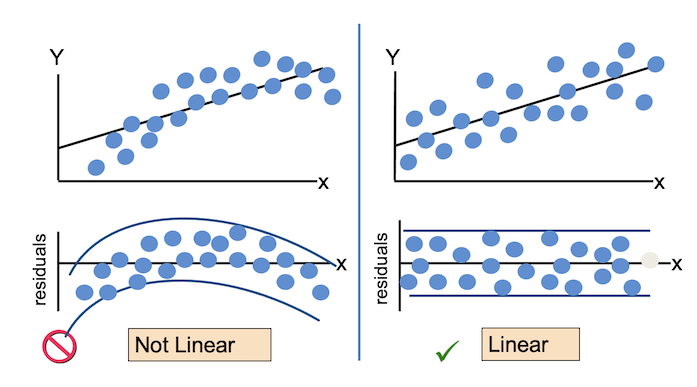
Normal Q-Q plots the ordered standardised residuals against their theoretical expectations. We expect these points to lie on a straight line, with significant deviation from a straight line indicating non-normality.
Scale-Location plots the square root of the standardised residuals (think of the square root of a measure of relative error) as a function of the fitted values. Again, there should be no obvious trend in this plot.
Point Leverage (Residuals vs Leverage) gives us a measure of importance of each point in determining the regression result. If any point in this plot falls outside of a Cook’s distance of 1 (indicated by the red dashed lines) then it is conventionally considered to be an influential observation.
Leverage Points
- Leverage points are observations which have an \(x\)-value that is distant from other \(x\)-values.
- These points have great influence on the fitted model, in that if they were to be removed from the data set and the model refitted, the resulting model would be significantly different from the original.
- Leverage points are bad if it is also an outlier (the \(y\)-value does not follow the pattern set by the other data points).
- Never remove data points unless we are certain that the data point is invalid and could not occur in real life.
- Otherwise, we should fit a different regression model if we are not confident that the basic linear model is suitable.
- We can create a different regression model by including higher-order terms or transforming the data.
Cook’s Distance
The Cook’s distance statistic \(D\) combines the effects of leverage and the magnitude of the residual and is used to evaluate the impact of a given observation on the estimated regression coefficient. As a rule of thumb, a point with Cook’s distance greater than 1 has undue influence on the model.
Statistical Tests for Model Assumptions
There are a number of statistical tests available from the lmtest package that can be used to test for violations of the assumptions of a linear model.
For the Breusch-Pagan test of homoscedesiticity, the null hypothesis is the variance is unchanging in the residual.
library(lmtest)
bptest(model1, ~ age, data = heart, studentize = FALSE)
##
## Breusch-Pagan test
##
## data: model1
## BP = 1.8038, df = 1, p-value = 0.1793
For the Breusch-Godfrey test for higher-order serial correlation, the null hypothesis is the residuals are independent.
library(lmtest)
bgtest(model1, order = 1, order.by = NULL, type = c("Chisq", "F"), data = list())
##
## Breusch-Godfrey test for serial correlation of order up to 1
##
## data: model1
## LM test = 0.41755, df = 1, p-value = 0.5182
For the Goldfeld-Quandt test against heteroscedasticity, the null hypothesis is the errors are homoscedastic (equal variance).
library(lmtest)
gqtest(model1, point = 0.5, fraction = 0, alternative = c("greater", "two.sided", "less"),
order.by = NULL, data = list())
##
## Goldfeld-Quandt test
##
## data: model1
## GQ = 1.2121, df1 = 48, df2 = 48, p-value = 0.2538
## alternative hypothesis: variance increases from segment 1 to 2
Each of these tests show that the models assumptions are met.
There are other packages you can use to test the assumptions of the model, such as the car library.
``qqPlot` gives us a QQ plot with 95% confidence intervals.
library(car)
qqPlot(model1, main = "QQ Plot")
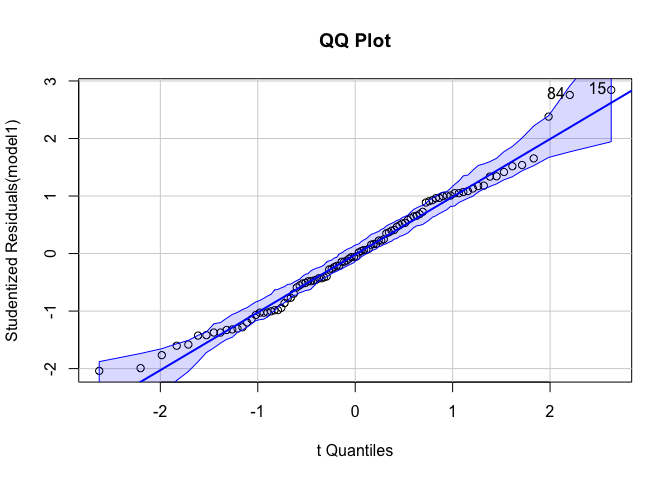
outlierTest tests for outliers and prints a p-value for the most extreme outlier.
outlierTest(model1)
## No Studentized residuals with Bonferroni p < 0.05
## Largest |rstudent|:
## rstudent unadjusted p-value Bonferroni p
## 15 2.84362 0.0054398 0.54398
In this case, we observe no significant outliers.
Exercise - SBP and Sex
In this exercise we will be exploring the relationship between systolic blood pressure (the dependent variable) and sex (the independent variable) using linear models. The main difference between this exercise and the last is that age is a numerical variable and sex is binary.
Comparing boxplots can give us a good indication if the distributions of SBP is different between males and females.
ggplot(data = heart, aes(x = sex, y = trestbps, fill = sex)) +
geom_boxplot()
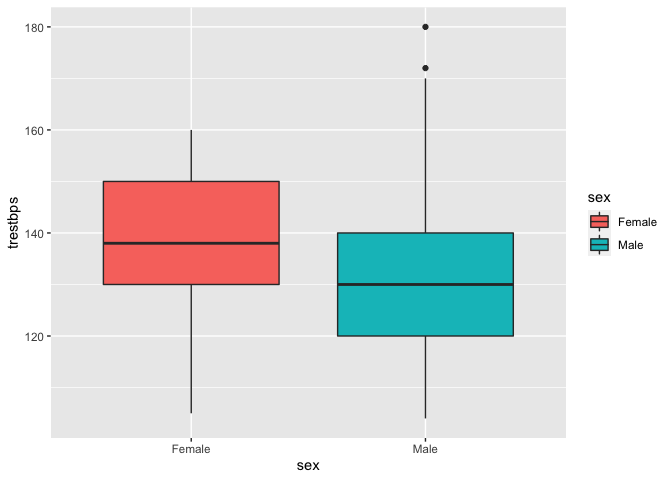
Visually, it seems that females on average have a higher systolic blood pressure than males.
The male distribution seems to be right-skewed.
We can test for normality for both variables using shapiro.test.
by(heart$trestbps, heart$sex, shapiro.test)
## heart$sex: Female
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.95866, p-value = 0.3046
##
## ------------------------------------------------------------
## heart$sex: Male
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.94999, p-value = 0.006713
We see here that there is significant evidence that the male dataset is non-normally distributed, and so we cannot use a t-test to determine if the means are different.
The Wilcoxon rank sum test, given by wilcox.test in R, is a non-parametric alternative to the unpaired two-samples t-test.
wilcox.test(heart$trestbps ~ heart$sex)
##
## Wilcoxon rank sum test with continuity correction
##
## data: heart$trestbps by heart$sex
## W = 1260, p-value = 0.07859
## alternative hypothesis: true location shift is not equal to 0
The p-value of approximately 0.08 indicates that male’s and female’s systolic blood pressure are not significantly different.
Now, let’s run a regression model to test the relationship between SBP and sex when SBP is considered as the outcome variable.
model_sex <- lm(trestbps ~ sex, data = heart)
summary(model_sex)
##
## Call:
## lm(formula = trestbps ~ sex, data = heart)
##
## Residuals:
## Min 1Q Median 3Q Max
## -31.76 -11.69 -1.69 8.31 48.31
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 136.759 2.869 47.664 <2e-16 ***
## sexMale -5.068 3.405 -1.488 0.14
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 15.45 on 98 degrees of freedom
## Multiple R-squared: 0.02211, Adjusted R-squared: 0.01213
## F-statistic: 2.216 on 1 and 98 DF, p-value: 0.1398
In this model, the first level of sex has been taken as reference (Females). We can think of females being assigned a value of 0 in the linear model and males a value of 1. Therefore, the model estimates that females, on average, have a systolic blood pressure of 136.76, and for males 136.76 - 5.07 = 131.69. However, we see that the p-value for the sex effect is not significant, and so we can conclude that there is no difference in SBP between men and women.
Again, we can view and report the confidence intervals for the model coefficients for the model using confint.
confint(model_sex)
## 2.5 % 97.5 %
## (Intercept) 131.06475 142.452488
## sexMale -11.82586 1.688897
And we can check the assumptions of the model by plotting the model diagnostics.
par(mfrow = c(2, 2))
plot(model_sex)
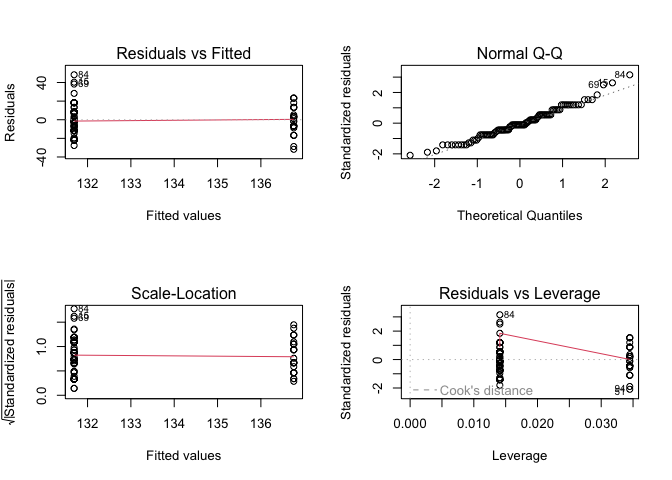
Intepreting these model diagnostics is a bit harder, as we are using a binary predictor and thus only fitted values for the entire dataset.
- The variance of the residuals appears to be similar between the sexes.
- Our normal Q-Q plot shows little deviation from a straight line.
- In our Residuals vs. Leverage plot, no points fall outside of Cook’s distance.
Key Points
Simple linear regression is for predicting the dependent variable Y based on one independent variable X.
R offers a large number of useful functions for performing linear regression.
Always check the model diagnostic plots and run the model diagnostic plots to check that the assumptions of linear regression are met.
Multiple Linear Regression
Overview
Teaching: 30 min
Exercises: 90 minQuestions
What is multiple linear regression?
What are the additional assumptions we need to meet to use multiple linear regression?
How do I perform multiple linear regression in R?
How do I ensure that my data meets the model assumptions?
Objectives
Extend our theory of simple linear regression to multiple linear regression.
Use multiple linear regression on our dataset.
Check the model diagnostics to ensure the data meets the assumptions of multiple linear regression.
In simple linear regression, we want to test the effect of one independent variable on one dependent variable. Multiple linear regression is an extension of simple linear regression and allows for multiple independent variables to predict the dependent variable.
Our simple linear regression model of cigarettes and coronary heart disease gave us that 50% of the variance in CHD could be explained by cigarette smoking. What about the other 50%? Maybe exercise or cholesterol?
As an extension of simple linear regression, the multiple linear regression model is very similar. If we have \(p\) independent variables, then our model is \(Y = a + b_1 X_1 + b_2 X_2 + \cdots + b_p X_p + e,\) where
- \(Y\) is the dependent or outcome variable
- \(a\) is again the estimated Y-intercept
- \(X_i\) is the value of the \(i\)th independent variable
- \(b_i\) is the estimated regression coefficient (effect size) of the \(i\)th independent variable
- \(e\) is the residual term.
Here, \(Y\) is a continuous variable and the independent variables \(X_i\) are either continuous or a binary value.
Each regression coefficient is the amount of change in the outcome variable that would be expected per one-unit change of the predictor, if all other variables in the model were held constant
Multivariable analysis can be used to control for confounder effects (e.g. to adjust for age), to test for interactions between predictors and to improve prediction.
Model Assumptions
Along with a few familiar assumptions from multiple regression (normality of residuals, homoscedasticity of residuals, outliers), there are a number of new assumptions to account for multiple independent variables.
Sample Size
The sample size should be at least 10 or 20 times the number of independent variables (\(n >> p\)) otherwise the estimates of the regression are unstable.
Multicollinearity
If two (independent) variables are closely related it is difficult to estimate their regression coefficients because they will both have a similar effect on the outcome. This difficulty is called collinearity. The solution to this problem is to exclude one of the highly correlated variables.
Overfitting
Related to our sample size assumption, in multivariable modeling, you can get highly significant but meaningless results if you put too many predictors in the model compared to the number of samples. This is known as overfitting, where the model is fit perfectly to the quirks of your particular sample, but has no predictive ability in a new sample. A common approach that controls over fitting by keeping the number of predictors to a minimum is step-wise multiple regression:
We start with the one predictor that explains the most predicted variance (i.e. has the highest correlation coefficient with the outcome). Next, the most statistically significant predictors is added to the model. The process is repeated until no remaining predictor has a statistically significant correlation with the outcome.
Similarly to simple linear regression, the coefficient of determination (\(R^2\)) indicates the percent of variance in the dependant variable explained by combined effects of the independent variables. The adjusted \(R^2\) is used for estimating explained variance in a population (not just the sample) when the sample size is small.
Outliers
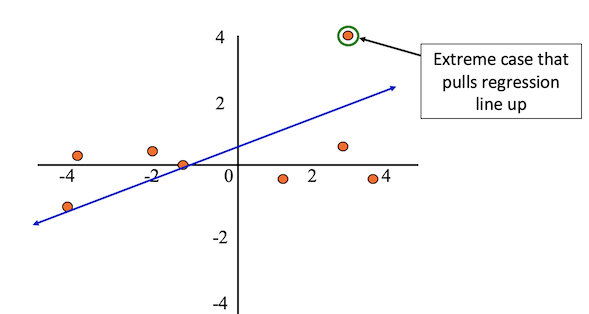
Outliers are observations with extreme values that differ greatly from the rest of your sample.
Even a few outliers can dramatically change estimates of the slope, \(b\).
The figure below shows an example dataset with an outlier.
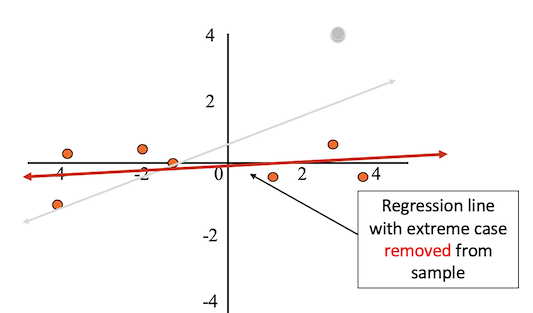
After removing the outlier from the sample, the regression line better fits the rest of the data.
Outliers can result from:
- Errors in coding or data entry (rectify the observation)
- Impossible values in real life (remove the observation)
- Or, sometimes they reflect important “real” variation (include - run the analysis both with and without the observation)
If you see no reason why your outliers are erroneous measurements, then there is no truly objective way to remove them.
Example - Does ignoring problems and worrying predict psychological distress?
Neill (2001)
Here, we will look into an example in the literature, where two predictor variables: “ignoring problems” and “worrying” were used in a multiple linear regression model to predict psychological distress. The study design is:
- \(n = 224\) participants (Australian adolescent population)
- \(Y\): Measure of psychological distress (low scores indicated a high level of psychological distress)
- \(X_1\): Worrying (score based on items)
- \(X_2\): Ignoring problems (score based on items)
Our model is:
[\text{PsychDistress} = a + b_1 \times (\text{Worrying}) + b_2 \times (\text{IgnoringProblems})]
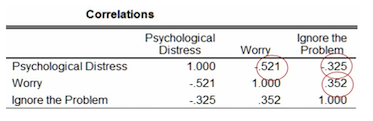
Correlations
The figure below shows the correlations between the three variables being assessed. We can see that the correlation between the independent variables is low (0.352), suggesting that multicollinearity may not be present in this data set. The correlations between the independent and dependent variables are negative (-0.521 and -0.325).
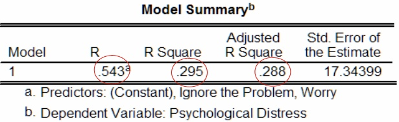
Model Summary and Coefficients
The figure below shows the \(R\), \(R^2\) and Adjusted \(R^2\) values after fitting the model. We have \(R^2 = 0.295\), which indicates that, under our model, approximately 30% of the variance in psychological distress can be attributed to the combined effects of ignoring the problem and worrying.
The estimated coefficients of the model is shown in the figure below.
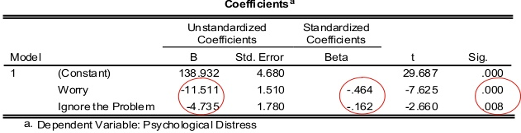
On the right hand side of the table we can see the p-value of each estimate
For each estimated effect, we wish to ask: Is there a linear relationship between each variable \(X_i\) and \(Y\)? The hypotheses for these tests are:
- \(H_0\): \(b_i = 0\) (no linear relationship)
- \(H_1\): \(b_i \neq 0\) (linear relationship between \(X_i\) and \(Y\))
We can see from the coefficients table that all estimates are highly significant.
The unstandardised coefficients give us our values of \(a = 138.93\), \(b_1 = -11.51\) and \(b_2 = -4.74\), and so our model is
[\text{PsychDistress} = 138.93 - 11.51 \times (\text{Worrying}) - 4.74 \times (\text{IgnoringProblems})]
We can make some interpretations of the model using these estimates:
- When the score of worrying and ignoring problems are both zero, then the psychological distress score is 138.93.
- When the score of ignoring problems is held constant, each unit increase in the score of not worrying decreases the psychological distress score by 11.51 units.
- When the score of worrying is held constant, each unit increase in the score of ignoring problems decreases the psychological distress score by 4.71 units.
The standardised coefficients (Beta) are calculated using the unstandardised coefficients and their respective standard error. These values allow us to compare the relative effect size of the predictor variables; here, we see that worrying has a relatively larger (negative) effect size.
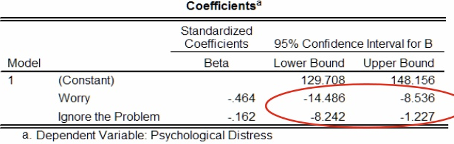
The figure below gives 95% confidence intervals for the intercept term and the standardised coefficients. We can interpret these intervals as: we can be 95% confident that the interval captures the true value of the estimate.
Non-linear Models
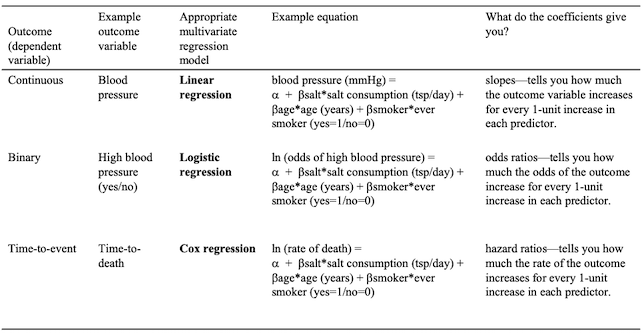
Linear Regression fits a straight line to your data, but in some cases a non-linear model may be more appropriate, such as logistic or cox regression. Non-linear models are usually used when non-linear relationships have some biological explanation.
Examples of Non-linear Models
Examples of different multivariate regression models are shown in the table below.
Summary
In summary, choose simple linear regression when you are predicting a continuous variable with one predictor variable, and choose multiple linear regression when predicting with more than one predictor variable.
Exercise 1 - Identify potential predictors of Systolic Blood Pressure
Step 1: Checking for correlations
First, we will check for correlations between our variables of interest.
n <- c("trestbps", "age", "chol", "thalach")
round(cor(heart[, n], method = "spearman", use = "pairwise.complete.obs"), 2)
## trestbps age chol thalach
## trestbps 1.00 0.27 0.21 -0.07
## age 0.27 1.00 0.29 -0.37
## chol 0.21 0.29 1.00 -0.01
## thalach -0.07 -0.37 -0.01 1.00
Here we observe that age and cholesterol have the highest correlations with SBP, and there are no high correlations within the predictor variables.
Step 2: Identifying potential predictors
Next, we will identify potential predictors of SBP in univariable linear regressions (i.e, SBP vs. each predictor). We can check this manually one-by-one, or in a loop.
We can manually fit a simple linear regression model for each predictor variable, with SBP as the dependent variable, and check the significance of the relationship to determine if the predictor variable should be included in the multivariable model. The example below does so for the age variable.
i <- "age"
anova(lm(heart$trestbps ~ heart[, i]))
## Analysis of Variance Table
##
## Response: heart$trestbps
## Df Sum Sq Mean Sq F value Pr(>F)
## heart[, i] 1 2380.9 2380.91 10.83 0.001389 **
## Residuals 98 21544.5 219.84
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
summary(lm(heart$trestbps ~ heart[, i]))
##
## Call:
## lm(formula = heart$trestbps ~ heart[, i])
##
## Residuals:
## Min 1Q Median 3Q Max
## -29.362 -11.385 -0.823 10.185 40.489
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 100.1066 10.1527 9.860 2.44e-16 ***
## heart[, i] 0.6039 0.1835 3.291 0.00139 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 14.83 on 98 degrees of freedom
## Multiple R-squared: 0.09951, Adjusted R-squared: 0.09033
## F-statistic: 10.83 on 1 and 98 DF, p-value: 0.001389
A more advanced and efficient method would be to perform these checks in a loop.
result_LM <- c()
N <- c(2:6)
for(i in N) {
res <- lm(heart$trestbps ~ heart[, i])
result_LM[i] <- anova(res)$`Pr(>F)`[1]
}
signfic_res_or_close <- colnames(heart)[which(result_LM < 0.2)]
print(signfic_res_or_close)
## [1] "age" "sex" "chol" "fbs"
Next, we will create a new dataset containing the predictors of interest along with the SBP and ID data using the signfic_res_or_close vector we just created.
newdataset <- heart[, c("ID", "trestbps", signfic_res_or_close)] # create a new dataset only containing the data we will use in the model
rownames(newdataset) <- newdataset$ID # set the row names to be the ID of the observations
newdataset <- newdataset[, -1] # remove the ID column from the data
Step 3: Fitting the model
Now we will fit the multiple linear regression model on the data of interest, using the same lm function from simple linear regression, and print the summary of the model.
result <- lm(trestbps ~ ., data = newdataset)
anova(result)
## Analysis of Variance Table
##
## Response: trestbps
## Df Sum Sq Mean Sq F value Pr(>F)
## age 1 2380.9 2380.91 11.2843 0.001126 **
## sex 1 264.5 264.51 1.2537 0.265678
## chol 1 268.5 268.47 1.2724 0.262159
## fbs 1 967.2 967.17 4.5839 0.034833 *
## Residuals 95 20044.4 210.99
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
summary(result)
##
## Call:
## lm(formula = trestbps ~ ., data = newdataset)
##
## Residuals:
## Min 1Q Median 3Q Max
## -25.385 -11.319 -1.913 10.158 34.460
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 102.26977 12.09094 8.458 3.23e-13 ***
## age 0.42890 0.19344 2.217 0.0290 *
## sexMale -3.43855 3.31865 -1.036 0.3028
## chol 0.03498 0.03189 1.097 0.2754
## fbs>120 9.49559 4.43511 2.141 0.0348 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 14.53 on 95 degrees of freedom
## Multiple R-squared: 0.1622, Adjusted R-squared: 0.1269
## F-statistic: 4.599 on 4 and 95 DF, p-value: 0.001943
The adjusted \(R^2\) is approximately 0.13, indicating that 13% of the variability in SBP is explained by the combination of all the independent variables included in the model. However, we can see that sex and cholesterol are not significant. We will use step-wise elimination to obtain a better model by removing a variable one-by-one.
One option is using the Akaike information criterion (AIC) to determine which model is best for the dataset. We can use step to do so.
step(result, direction = "backward") #Base R
## Start: AIC=540.05
## trestbps ~ age + sex + chol + fbs
##
## Df Sum of Sq RSS AIC
## - sex 1 226.51 20271 539.18
## - chol 1 253.92 20298 539.31
## <none> 20044 540.05
## - fbs 1 967.17 21012 542.77
## - age 1 1037.31 21082 543.10
##
## Step: AIC=539.18
## trestbps ~ age + chol + fbs
##
## Df Sum of Sq RSS AIC
## - chol 1 381.24 20652 539.04
## <none> 20271 539.18
## - fbs 1 896.27 21167 541.50
## - age 1 1135.49 21406 542.63
##
## Step: AIC=539.04
## trestbps ~ age + fbs
##
## Df Sum of Sq RSS AIC
## <none> 20652 539.04
## - fbs 1 892.39 21544 541.27
## - age 1 1711.17 22363 545.00
##
## Call:
## lm(formula = trestbps ~ age + fbs, data = newdataset)
##
## Coefficients:
## (Intercept) age fbs>120
## 103.3074 0.5239 9.0886
Alternatively, we can use the MASS library’s stepAIC function.
library(MASS)
stepAIC(result, direction = "backward") #library MASS
## Start: AIC=540.05
## trestbps ~ age + sex + chol + fbs
##
## Df Sum of Sq RSS AIC
## - sex 1 226.51 20271 539.18
## - chol 1 253.92 20298 539.31
## <none> 20044 540.05
## - fbs 1 967.17 21012 542.77
## - age 1 1037.31 21082 543.10
##
## Step: AIC=539.18
## trestbps ~ age + chol + fbs
##
## Df Sum of Sq RSS AIC
## - chol 1 381.24 20652 539.04
## <none> 20271 539.18
## - fbs 1 896.27 21167 541.50
## - age 1 1135.49 21406 542.63
##
## Step: AIC=539.04
## trestbps ~ age + fbs
##
## Df Sum of Sq RSS AIC
## <none> 20652 539.04
## - fbs 1 892.39 21544 541.27
## - age 1 1711.17 22363 545.00
##
## Call:
## lm(formula = trestbps ~ age + fbs, data = newdataset)
##
## Coefficients:
## (Intercept) age fbs>120
## 103.3074 0.5239 9.0886
In both functions, the call of the final model is outputted. Let’s have a look at the summary.
finalmodel <- lm(trestbps ~ age + fbs, data = newdataset)
summary(finalmodel)
##
## Call:
## lm(formula = trestbps ~ age + fbs, data = newdataset)
##
## Residuals:
## Min 1Q Median 3Q Max
## -27.36 -10.81 -0.14 10.12 35.78
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 103.3074 10.1129 10.215 < 2e-16 ***
## age 0.5239 0.1848 2.835 0.00558 **
## fbs>120 9.0886 4.4393 2.047 0.04333 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 14.59 on 97 degrees of freedom
## Multiple R-squared: 0.1368, Adjusted R-squared: 0.119
## F-statistic: 7.687 on 2 and 97 DF, p-value: 0.0007963
Now, with all estimates significant, we can make some interpretations:
- SBP increases by 0.52 units for every unit increase of age when all other variables in the model are kept constant.
- SBP is estimated to be 9.90 units higher for participants with fbs > 120 than those with fbs < 120 when all other variables in the model are kept constant.
However, we still need to check the assumptions of a multiple linear regression model are met before using the model.
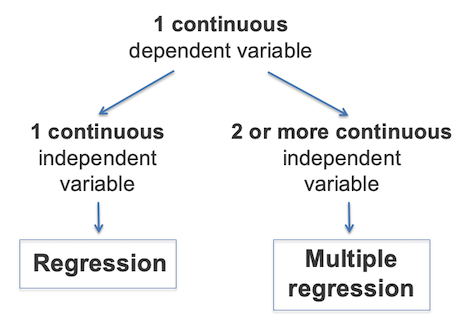
Step 4: Checking the assumptions
par(mfrow = c(2, 2))
plot(finalmodel)
Here, we observe that the variance of the residuals seems constant and the distribution of the residuals appears to be normal.
To measure multicolinearity, we can use the vif function from the car package.
VIF measures how much the variance of any one of the coefficients is inflated due to multicollinearity in the overall model.
As a rule of thumb, any value above 5 is a cause for concern.
library(car)
car::vif(finalmodel)
## age fbs
## 1.0469 1.0469
There appears to be no evidence of colinearity, and so we can conclude that the assumptions of the model are met.
Another approach - a priori selection of variables.
An alternative approach is to simply include all variables determined to be important.
First, we select all variables of interest and fit the model.
selection <- c("ID", "age", "sex", "chol", "trestbps", "fbs", "thalach")
select_data <- heart[, selection]
rownames(select_data) <- select_data$ID
select_data <- select_data[,-1]
result2 <- lm(trestbps ~ ., data = select_data) # . means add all variables except for the specified dependent variable
anova(result2)
## Analysis of Variance Table
##
## Response: trestbps
## Df Sum Sq Mean Sq F value Pr(>F)
## age 1 2380.9 2380.91 11.1687 0.001195 **
## sex 1 264.5 264.51 1.2408 0.268154
## chol 1 268.5 268.47 1.2594 0.264630
## fbs 1 967.2 967.17 4.5370 0.035782 *
## thalach 1 5.8 5.80 0.0272 0.869319
## Residuals 94 20038.6 213.18
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
summary(result2)
##
## Call:
## lm(formula = trestbps ~ ., data = select_data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -25.140 -11.395 -1.931 10.165 34.450
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 104.85347 19.82376 5.289 7.98e-07 ***
## age 0.41491 0.21213 1.956 0.0534 .
## sexMale -3.47769 3.34420 -1.040 0.3010
## chol 0.03574 0.03238 1.104 0.2725
## fbs>120 9.60786 4.50964 2.131 0.0357 *
## thalach -0.01310 0.07941 -0.165 0.8693
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 14.6 on 94 degrees of freedom
## Multiple R-squared: 0.1625, Adjusted R-squared: 0.1179
## F-statistic: 3.647 on 5 and 94 DF, p-value: 0.004644
The interpretation of the model estimates are:
- SBP level equals 104.9 mmHg when all the other variables in the model equal zero (note: this doesn’t make sense in real life given the nature of the variables)
- SBP increases by 0.41 units for each unit increase of age
- SBP level is 9.6 units higher in patients with fbs greater than 120 as compared to those with fbs less than 120 units.
As always, we must check the assumptions of the model. First, we look at multicolinearity.
car::vif(result2)
## age sex chol fbs thalach
## 1.377895 1.080196 1.175630 1.078965 1.196628
As there are no values above 5, there appears to be no evidence of multicolinearity.
Next, we check the other assumptions.
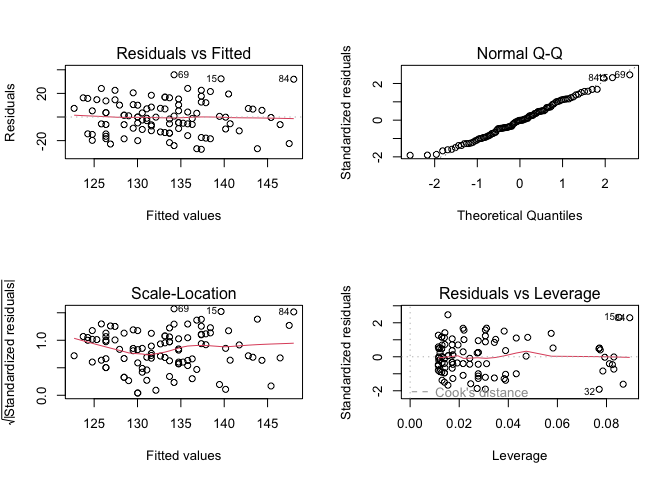
par(mfrow = c(2, 2))
plot(result2)
The variance of the residuals appears constant and the distribution of the residuals appear normal. However, despite adding more variables, this model explains 12% variability (\(R^2 = 0.117\)) in the outcome as compared to 13% from the other model. Some variables that had significant effect in the other model are now insignificant (age, sex), which limits the interpretability of the model.
A more robust approach, such as stepwise or lasso regression, could be used to select the final model.
Exercise 2 - Identifying potential predictors of plasma beta-carotene level
Data not published yet but a related reference is: Nierenberg DW, Stukel TA, Baron JA, Dain BJ, Greenberg ER. Determinants of plasma levels of beta-carotene and retinol. American Journal of Epidemiology 1989;130:511-521
For this exercise, we will use multiple linear regression to identify determinants of plasma beta-carotene levels. The data we will use is from a cross-sectional study investigating the relationship between personal characteristics and dietary factors, and plasma concentrations of beta-carotene. This study observed 315 patients who had a surgical procedure to remove a non-cancerous lesion of the lung, colon, breast, skin, ovary or uterus.
| Variable | Description |
|---|---|
| age | Age (years) |
| sex | Sex (1 = male, 2 = female) |
| smokstat | Smoking status (1 = never, 2 = former, 3 = current Smoker) |
| quetelet | Quetelet (weight/height2) |
| vituse | Vitamin use (1 = yes, fairly often, 2 = yes, not often, 3 = no) |
| calories | Number of calories consumed per day |
| fat | Grams of fat consumed per day |
| fiber | Grams of fiber consumed per day |
| alcohol | Number of alcoholic drinks consumed per week |
| cholesterol | Cholestoral consumed (mg per day) |
| betadiet | Dietary beta-carotene consumed (µg per day) |
| retdiet | Dietary retinol consumed (µg per day) |
| betaplasma | Plasma beta-carotene (ng/ml) |
| retplasma | Plasma retinol (ng/ml) |
Importing and cleaning the data
First, we will import the data and use the str function to check its coding.
plasma <- read.csv("data/plasma.csv", stringsAsFactors = TRUE)
str(plasma)
## 'data.frame': 315 obs. of 15 variables:
## $ Patient.ID : int 1 2 3 4 5 6 7 8 9 10 ...
## $ age : int 64 76 38 40 72 40 65 58 35 55 ...
## $ sex : int 2 2 2 2 2 2 2 2 2 2 ...
## $ smokstat : int 2 1 2 2 1 2 1 1 1 2 ...
## $ quetelet : num 21.5 23.9 20 25.1 21 ...
## $ vituse : int 1 1 2 3 1 3 2 1 3 3 ...
## $ calories : num 1299 1032 2372 2450 1952 ...
## $ fat : num 57 50.1 83.6 97.5 82.6 56 52 63.4 57.8 39.6 ...
## $ fiber : num 6.3 15.8 19.1 26.5 16.2 9.6 28.7 10.9 20.3 15.5 ...
## $ alcohol : num 0 0 14.1 0.5 0 1.3 0 0 0.6 0 ...
## $ cholesterol: num 170.3 75.8 257.9 332.6 170.8 ...
## $ betadiet : int 1945 2653 6321 1061 2863 1729 5371 823 2895 3307 ...
## $ retdiet : int 890 451 660 864 1209 1439 802 2571 944 493 ...
## $ betaplasma : int 200 124 328 153 92 148 258 64 218 81 ...
## $ retplasma : int 915 727 721 615 799 654 834 825 517 562 ...
As with our systolic blood pressure example, we have categorical variables being coded as numerical values, and so we will change them to factors.
plasma$Patient.ID <- as.factor(plasma$Patient.ID)
plasma$sex <- as.factor(plasma$sex)
plasma$smokstat <- as.factor(plasma$smokstat)
plasma$vituse <- as.factor(plasma$vituse)
To aid in interpreting the model, we will change the levels of the factors, where appropriate.
levels(plasma$sex) <- c("Male", "Female")
levels(plasma$smokstat) <- c("Never", "Former", "Current")
levels(plasma$vituse) <- c("Often", "NotOften", "No")
Now we can view a summary of the data with the correct variable types.
summary(plasma)
## Patient.ID age sex smokstat quetelet
## 1 : 1 Min. :19.00 Male : 42 Never :157 Min. :16.33
## 2 : 1 1st Qu.:39.00 Female:273 Former :115 1st Qu.:21.80
## 3 : 1 Median :48.00 Current: 43 Median :24.74
## 4 : 1 Mean :50.15 Mean :26.16
## 5 : 1 3rd Qu.:62.50 3rd Qu.:28.85
## 6 : 1 Max. :83.00 Max. :50.40
## (Other):309
## vituse calories fat fiber
## Often :122 Min. : 445.2 Min. : 14.40 Min. : 3.10
## NotOften: 82 1st Qu.:1338.0 1st Qu.: 53.95 1st Qu.: 9.15
## No :111 Median :1666.8 Median : 72.90 Median :12.10
## Mean :1796.7 Mean : 77.03 Mean :12.79
## 3rd Qu.:2100.4 3rd Qu.: 95.25 3rd Qu.:15.60
## Max. :6662.2 Max. :235.90 Max. :36.80
##
## alcohol cholesterol betadiet retdiet
## Min. : 0.000 Min. : 37.7 Min. : 214 Min. : 30.0
## 1st Qu.: 0.000 1st Qu.:155.0 1st Qu.:1116 1st Qu.: 480.0
## Median : 0.300 Median :206.3 Median :1802 Median : 707.0
## Mean : 2.643 Mean :242.5 Mean :2186 Mean : 832.7
## 3rd Qu.: 3.200 3rd Qu.:308.9 3rd Qu.:2836 3rd Qu.:1037.0
## Max. :35.000 Max. :900.7 Max. :9642 Max. :6901.0
## NA's :1
## betaplasma retplasma
## Min. : 0.0 Min. : 179.0
## 1st Qu.: 90.0 1st Qu.: 466.0
## Median : 140.0 Median : 566.0
## Mean : 189.9 Mean : 602.8
## 3rd Qu.: 230.0 3rd Qu.: 716.0
## Max. :1415.0 Max. :1727.0
##
Let’s view a histogram of the plasma beta-carotene variable.
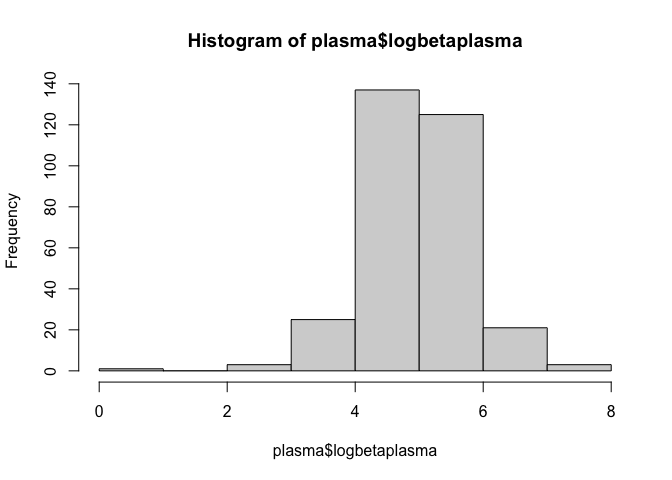
hist(plasma$betaplasma)
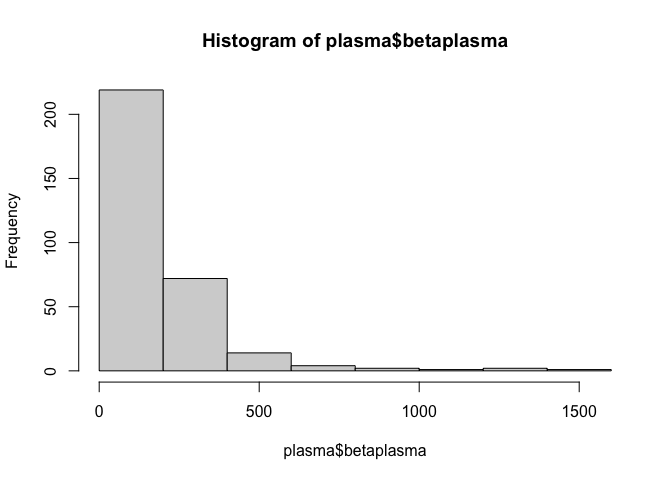
This doesn’t appear to be normally distributed, which may affect the performance of our model. We can check this using the Shapiro-Wilk normality test.
shapiro.test(plasma$betaplasma)
##
## Shapiro-Wilk normality test
##
## data: plasma$betaplasma
## W = 0.66071, p-value < 2.2e-16
This tiny p-value suggests it is incredibly unlikely that the data is normally distributed. However, the data is right-skewed, as shown below, which could mean that the data is log-normally distributed.
Under this distribution, the logarithm of the data is normally distributed.
Other transformations include:
- When the data are counts, perform a square-root transformation:
[x_{\text{trans}} = \sqrt{x + 1/2}]
- When data are proportions, perform an arcsine transformation
[x_{\text{trans}} = \arcsin(\sqrt{x})]
- When frequency distribution of data is left-skewed, perform a square transformation:
[x_{\text{trans}} = x^2]
Using the log function, we will create a new variable for plasma beta-carotene with a log-transformation applied and plot a histogram for this new variable.
plasma$logbetaplasma <- log(plasma$betaplasma + 1)
hist(plasma$logbetaplasma)
Checking for correlations
Next, we will check for correlations between beta-carotene and the potential independent variables.
n <- as.vector(which(sapply(plasma, is.numeric)))
cor(plasma$betaplasma, plasma[, n], method = "spearman", use = "pairwise.complete.obs")
## age quetelet calories fat fiber alcohol
## [1,] 0.1596575 -0.2969552 -0.0552741 -0.1311411 0.1890558 0.07566391
## cholesterol betadiet retdiet betaplasma retplasma logbetaplasma
## [1,] -0.142528 0.1786116 0.02242424 1 0.1306213 1
Here, we observe quetelet (-), cholesterol (-), betadiet (+) and fiber (+) have the highest correlations with betaplasma.
Regression with untransformed beta-carotene
As in our previous example, we will identify potential predictors of beta-carotene in univariate linear regression. As we are now R experts, we will do so using the advanced option!
result_LM <- c()
N <- c(2:13)
for(i in N) {
res <- lm(plasma$betaplasma ~ plasma[, i])
result_LM[i] <- anova(res)$`Pr(>F)`[1]
}
signfic_res_or_close <- colnames(plasma)[which(result_LM < 0.2)]
print(signfic_res_or_close)
## [1] "age" "sex" "smokstat" "quetelet" "vituse"
## [6] "fat" "fiber" "cholesterol" "betadiet"
Fitting the model
Now that we have the predictor variables of interest, we can fit our initial model.
signif <- c("Patient.ID", "age", "sex", "smokstat", "quetelet", "vituse", "fat", "fiber", "cholesterol", "betadiet")
newdataset <- plasma[ , c(signif, "betaplasma")]
rownames(newdataset) <- newdataset$Patient.ID
newdataset <- newdataset[,-1]
#Conduct multiple linear regression on initially selected variables
initial_result <- lm(betaplasma ~ ., data = newdataset)
summary(initial_result)
##
## Call:
## lm(formula = betaplasma ~ ., data = newdataset)
##
## Residuals:
## Min 1Q Median 3Q Max
## -248.83 -91.86 -28.50 39.52 1074.67
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 270.244199 80.373812 3.362 0.000872 ***
## age 0.829072 0.714955 1.160 0.247119
## sexFemale 28.924845 31.135740 0.929 0.353633
## smokstatFormer -4.619008 21.103312 -0.219 0.826894
## smokstatCurrent -44.407926 30.583897 -1.452 0.147535
## quetelet -6.059352 1.616615 -3.748 0.000213 ***
## vituseNotOften -33.121372 24.378300 -1.359 0.175271
## vituseNo -75.123429 22.668202 -3.314 0.001031 **
## fat -0.294250 0.416752 -0.706 0.480696
## fiber 5.062592 2.139125 2.367 0.018578 *
## cholesterol -0.101467 0.104350 -0.972 0.331641
## betadiet 0.016869 0.007402 2.279 0.023358 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 167.4 on 303 degrees of freedom
## Multiple R-squared: 0.1924, Adjusted R-squared: 0.163
## F-statistic: 6.561 on 11 and 303 DF, p-value: 8.048e-10
We can see that there are many insignificant predictor variables. To find a better model, we will use backward elimination.
step(initial_result, direction = "backward")
## Start: AIC=3237.68
## betaplasma ~ age + sex + smokstat + quetelet + vituse + fat +
## fiber + cholesterol + betadiet
##
## Df Sum of Sq RSS AIC
## - smokstat 2 61227 8554072 3235.9
## - fat 1 13973 8506818 3236.2
## - sex 1 24190 8517035 3236.6
## - cholesterol 1 26502 8519347 3236.7
## - age 1 37691 8530536 3237.1
## <none> 8492845 3237.7
## - betadiet 1 145589 8638434 3241.0
## - fiber 1 156994 8649839 3241.5
## - vituse 2 308129 8800974 3244.9
## - quetelet 1 393776 8886621 3250.0
##
## Step: AIC=3235.94
## betaplasma ~ age + sex + quetelet + vituse + fat + fiber + cholesterol +
## betadiet
##
## Df Sum of Sq RSS AIC
## - fat 1 17973 8572045 3234.6
## - sex 1 29033 8583105 3235.0
## - cholesterol 1 29671 8583743 3235.0
## - age 1 52596 8606668 3235.9
## <none> 8554072 3235.9
## - betadiet 1 152640 8706712 3239.5
## - fiber 1 193347 8747419 3241.0
## - vituse 2 350499 8904571 3244.6
## - quetelet 1 358772 8912844 3246.9
##
## Step: AIC=3234.6
## betaplasma ~ age + sex + quetelet + vituse + fiber + cholesterol +
## betadiet
##
## Df Sum of Sq RSS AIC
## - sex 1 32104 8604149 3233.8
## <none> 8572045 3234.6
## - age 1 64663 8636707 3235.0
## - cholesterol 1 124969 8697014 3237.2
## - betadiet 1 154279 8726324 3238.2
## - fiber 1 176490 8748535 3239.0
## - vituse 2 356475 8928520 3243.4
## - quetelet 1 356325 8928369 3245.4
##
## Step: AIC=3233.78
## betaplasma ~ age + quetelet + vituse + fiber + cholesterol +
## betadiet
##
## Df Sum of Sq RSS AIC
## - age 1 43584 8647733 3233.4
## <none> 8604149 3233.8
## - betadiet 1 161688 8765836 3237.6
## - fiber 1 173266 8777414 3238.1
## - cholesterol 1 182098 8786247 3238.4
## - vituse 2 396774 9000923 3244.0
## - quetelet 1 351079 8955227 3244.4
##
## Step: AIC=3233.37
## betaplasma ~ quetelet + vituse + fiber + cholesterol + betadiet
##
## Df Sum of Sq RSS AIC
## <none> 8647733 3233.4
## - betadiet 1 172718 8820451 3237.6
## - fiber 1 178187 8825920 3237.8
## - cholesterol 1 208138 8855871 3238.9
## - vituse 2 393625 9041358 3243.4
## - quetelet 1 349446 8997179 3243.9
##
## Call:
## lm(formula = betaplasma ~ quetelet + vituse + fiber + cholesterol +
## betadiet, data = newdataset)
##
## Coefficients:
## (Intercept) quetelet vituseNotOften vituseNo fiber
## 318.98140 -5.63336 -39.06075 -83.16795 5.17640
## cholesterol betadiet
## -0.19938 0.01825
So, our final model uses quetelet, vitamin use, fiber, cholesterol and dietary beta-carotene as the predictor variables.
finalmodel_raw <- lm(formula = betaplasma ~ quetelet + vituse + fiber + cholesterol + betadiet, data = newdataset)
summary(finalmodel_raw)
##
## Call:
## lm(formula = betaplasma ~ quetelet + vituse + fiber + cholesterol +
## betadiet, data = newdataset)
##
## Residuals:
## Min 1Q Median 3Q Max
## -302.53 -89.27 -26.04 35.89 1075.58
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 318.981399 51.639159 6.177 2.06e-09 ***
## quetelet -5.633362 1.596810 -3.528 0.000483 ***
## vituseNotOften -39.060747 24.059922 -1.623 0.105510
## vituseNo -83.167948 22.213960 -3.744 0.000216 ***
## fiber 5.176397 2.054779 2.519 0.012268 *
## cholesterol -0.199382 0.073229 -2.723 0.006844 **
## betadiet 0.018248 0.007357 2.480 0.013664 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 167.6 on 308 degrees of freedom
## Multiple R-squared: 0.1776, Adjusted R-squared: 0.1616
## F-statistic: 11.09 on 6 and 308 DF, p-value: 3.37e-11
Finally, as always, we will check if the model meets the assumptions of multiple linear regression.
par(mfrow = c(2, 2))
plot(finalmodel_raw)
Here, we observe non-constant residual variance and deviation of residuals from normality. Let’s refit a model using the log-transformed plasma beta-carotene.
First, we obtain the significant variables from running seperate univariate linear regression models on each candidate predictor variable.
result_LM <- c()
N <- c(2:13)
for(i in N) {
res <- lm(plasma$logbetaplasma ~ plasma[, i])
result_LM[i] <- anova(res)$`Pr(>F)`[1]
}
signfic_res_or_close <- colnames(plasma)[which(result_LM < 0.2)]
Next, we fit an initial model using the significant variables and then perform backwards elimination to obtain the final model
signif <- c("Patient.ID", "age", "sex", "quetelet", "vituse", "smokstat", "fat", "fiber", "cholesterol", "betadiet")
newdataset <- plasma[ , c(signif, "logbetaplasma")]
rownames(newdataset) <- newdataset$Patient.ID
newdataset <- newdataset[,-1]
#Conduct multiple linear regression on initially selected variables
initial_result <- lm(logbetaplasma ~ ., data = newdataset)
summary(initial_result)
##
## Call:
## lm(formula = logbetaplasma ~ ., data = newdataset)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.0438 -0.3629 0.0272 0.3968 1.8536
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.408e+00 3.353e-01 16.129 < 2e-16 ***
## age 5.981e-03 2.983e-03 2.005 0.0458 *
## sexFemale 1.506e-01 1.299e-01 1.160 0.2471
## quetelet -3.230e-02 6.745e-03 -4.788 2.63e-06 ***
## vituseNotOften 2.614e-02 1.017e-01 0.257 0.7973
## vituseNo -2.425e-01 9.457e-02 -2.564 0.0108 *
## smokstatFormer -5.665e-02 8.804e-02 -0.643 0.5205
## smokstatCurrent -2.397e-01 1.276e-01 -1.879 0.0612 .
## fat -8.015e-04 1.739e-03 -0.461 0.6451
## fiber 2.161e-02 8.925e-03 2.421 0.0161 *
## cholesterol -1.100e-03 4.353e-04 -2.528 0.0120 *
## betadiet 6.548e-05 3.088e-05 2.120 0.0348 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6985 on 303 degrees of freedom
## Multiple R-squared: 0.2468, Adjusted R-squared: 0.2195
## F-statistic: 9.026 on 11 and 303 DF, p-value: 6.109e-14
#Backward Elimination
step(initial_result, direction = "backward")
## Start: AIC=-214.31
## logbetaplasma ~ age + sex + quetelet + vituse + smokstat + fat +
## fiber + cholesterol + betadiet
##
## Df Sum of Sq RSS AIC
## - fat 1 0.1037 147.93 -216.09
## - sex 1 0.6560 148.48 -214.92
## - smokstat 2 1.7226 149.55 -214.66
## <none> 147.82 -214.31
## - age 1 1.9618 149.79 -212.16
## - betadiet 1 2.1935 150.02 -211.67
## - fiber 1 2.8597 150.69 -210.28
## - cholesterol 1 3.1172 150.94 -209.74
## - vituse 2 4.3545 152.18 -209.17
## - quetelet 1 11.1863 159.01 -193.33
##
## Step: AIC=-216.09
## logbetaplasma ~ age + sex + quetelet + vituse + smokstat + fiber +
## cholesterol + betadiet
##
## Df Sum of Sq RSS AIC
## - sex 1 0.6832 148.61 -216.64
## - smokstat 2 1.7991 149.73 -216.28
## <none> 147.93 -216.09
## - age 1 2.1465 150.07 -213.55
## - betadiet 1 2.2133 150.14 -213.41
## - fiber 1 2.7635 150.69 -212.26
## - vituse 2 4.4042 152.33 -210.85
## - cholesterol 1 7.0665 155.00 -203.39
## - quetelet 1 11.1830 159.11 -195.13
##
## Step: AIC=-216.64
## logbetaplasma ~ age + quetelet + vituse + smokstat + fiber +
## cholesterol + betadiet
##
## Df Sum of Sq RSS AIC
## <none> 148.61 -216.64
## - smokstat 2 2.0143 150.63 -216.40
## - age 1 1.6077 150.22 -215.25
## - betadiet 1 2.3625 150.97 -213.67
## - fiber 1 2.6746 151.29 -213.02
## - vituse 2 5.0560 153.67 -210.10
## - cholesterol 1 9.1217 157.73 -199.87
## - quetelet 1 11.1350 159.75 -195.88
##
## Call:
## lm(formula = logbetaplasma ~ age + quetelet + vituse + smokstat +
## fiber + cholesterol + betadiet, data = newdataset)
##
## Coefficients:
## (Intercept) age quetelet vituseNotOften
## 5.604e+00 5.076e-03 -3.222e-02 3.011e-02
## vituseNo smokstatFormer smokstatCurrent fiber
## -2.571e-01 -7.415e-02 -2.562e-01 2.027e-02
## cholesterol betadiet
## -1.344e-03 6.783e-05
Notice that our final model using the log-transformation includes a different set of variables than the model with no transformation.
finalmodel <- lm(formula = logbetaplasma ~ age + quetelet + vituse + smokstat +
fiber + cholesterol + betadiet, data = newdataset)
summary(finalmodel)
##
## Call:
## lm(formula = logbetaplasma ~ age + quetelet + vituse + smokstat +
## fiber + cholesterol + betadiet, data = newdataset)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.9520 -0.3515 0.0174 0.4015 1.8709
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.604e+00 2.697e-01 20.780 < 2e-16 ***
## age 5.076e-03 2.794e-03 1.816 0.07029 .
## quetelet -3.222e-02 6.740e-03 -4.780 2.72e-06 ***
## vituseNotOften 3.011e-02 1.016e-01 0.296 0.76716
## vituseNo -2.571e-01 9.378e-02 -2.741 0.00648 **
## smokstatFormer -7.415e-02 8.685e-02 -0.854 0.39389
## smokstatCurrent -2.562e-01 1.267e-01 -2.021 0.04414 *
## fiber 2.027e-02 8.653e-03 2.343 0.01978 *
## cholesterol -1.344e-03 3.106e-04 -4.327 2.05e-05 ***
## betadiet 6.783e-05 3.081e-05 2.202 0.02842 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.698 on 305 degrees of freedom
## Multiple R-squared: 0.2428, Adjusted R-squared: 0.2204
## F-statistic: 10.87 on 9 and 305 DF, p-value: 1.144e-14
From reading the summary, we can see:
- logbetaplasma decreases by 0.03 units for every unit increase of quetelet
- logbetaplasma decreases by 0.26 units for patients not using vitamins as opposed to using them often
- logbetaplasma decreases by 0.26 units for smokers versus non-smoker
Let’s take a look at our diagnostic plots.
par(mfrow = c(2, 2))
plot(finalmodel)
The residuals look much better with the transformation, however, observation 257 appears to be an outlier. Let’s look at the data to see if there’s anything strange.
plasma[257,]
## Patient.ID age sex smokstat quetelet vituse calories fat fiber alcohol
## 257 257 40 Female Never 31.24219 Often 3014.9 165.7 14.4 0
## cholesterol betadiet retdiet betaplasma retplasma logbetaplasma
## 257 900.7 1028 3061 0 254 0
This observation has a plasma-beta level of 0, which is not possible in real life. So, we should remove this observation and refit the data.
plasma_no_na <- na.omit(plasma)
n <- which(plasma_no_na$Patient.ID == "257")
plasma_no_na <- plasma_no_na[-n,]
plasma_no_na$logbetaplasma <- log(plasma_no_na$betaplasma) # don't need +1 anymore as the 0 value has been removed
finalmodel <- lm(formula = logbetaplasma ~ age + quetelet + vituse + smokstat +
fiber + cholesterol + betadiet, data = plasma_no_na)
summary(finalmodel)
##
## Call:
## lm(formula = logbetaplasma ~ age + quetelet + vituse + smokstat +
## fiber + cholesterol + betadiet, data = plasma_no_na)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.05441 -0.37130 -0.02836 0.40989 1.91314
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.560e+00 2.574e-01 21.598 < 2e-16 ***
## age 4.807e-03 2.671e-03 1.800 0.072918 .
## quetelet -3.200e-02 6.422e-03 -4.983 1.05e-06 ***
## vituseNotOften -1.161e-02 9.696e-02 -0.120 0.904783
## vituseNo -2.999e-01 8.962e-02 -3.347 0.000921 ***
## smokstatFormer -1.093e-01 8.288e-02 -1.319 0.188108
## smokstatCurrent -3.145e-01 1.217e-01 -2.584 0.010231 *
## fiber 2.051e-02 8.244e-03 2.488 0.013396 *
## cholesterol -7.940e-04 3.132e-04 -2.535 0.011752 *
## betadiet 5.264e-05 2.945e-05 1.788 0.074843 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6646 on 303 degrees of freedom
## Multiple R-squared: 0.2345, Adjusted R-squared: 0.2118
## F-statistic: 10.31 on 9 and 303 DF, p-value: 6.794e-14
step(finalmodel, direction = "backward")
## Start: AIC=-245.95
## logbetaplasma ~ age + quetelet + vituse + smokstat + fiber +
## cholesterol + betadiet
##
## Df Sum of Sq RSS AIC
## <none> 133.82 -245.95
## - betadiet 1 1.4113 135.23 -244.67
## - age 1 1.4303 135.25 -244.62
## - smokstat 2 3.0718 136.89 -242.85
## - fiber 1 2.7332 136.56 -241.62
## - cholesterol 1 2.8379 136.66 -241.38
## - vituse 2 5.9915 139.81 -236.24
## - quetelet 1 10.9664 144.79 -223.30
##
## Call:
## lm(formula = logbetaplasma ~ age + quetelet + vituse + smokstat +
## fiber + cholesterol + betadiet, data = plasma_no_na)
##
## Coefficients:
## (Intercept) age quetelet vituseNotOften
## 5.560e+00 4.807e-03 -3.200e-02 -1.161e-02
## vituseNo smokstatFormer smokstatCurrent fiber
## -2.999e-01 -1.093e-01 -3.145e-01 2.051e-02
## cholesterol betadiet
## -7.940e-04 5.264e-05
res <- lm(formula = logbetaplasma ~ age + quetelet + vituse + smokstat +
fiber + cholesterol + betadiet, data = plasma_no_na)
summary(res)
##
## Call:
## lm(formula = logbetaplasma ~ age + quetelet + vituse + smokstat +
## fiber + cholesterol + betadiet, data = plasma_no_na)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.05441 -0.37130 -0.02836 0.40989 1.91314
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.560e+00 2.574e-01 21.598 < 2e-16 ***
## age 4.807e-03 2.671e-03 1.800 0.072918 .
## quetelet -3.200e-02 6.422e-03 -4.983 1.05e-06 ***
## vituseNotOften -1.161e-02 9.696e-02 -0.120 0.904783
## vituseNo -2.999e-01 8.962e-02 -3.347 0.000921 ***
## smokstatFormer -1.093e-01 8.288e-02 -1.319 0.188108
## smokstatCurrent -3.145e-01 1.217e-01 -2.584 0.010231 *
## fiber 2.051e-02 8.244e-03 2.488 0.013396 *
## cholesterol -7.940e-04 3.132e-04 -2.535 0.011752 *
## betadiet 5.264e-05 2.945e-05 1.788 0.074843 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6646 on 303 degrees of freedom
## Multiple R-squared: 0.2345, Adjusted R-squared: 0.2118
## F-statistic: 10.31 on 9 and 303 DF, p-value: 6.794e-14
Finally, checking the model plot diagnostics, we see that this model does not appear to violate any assumptions of multiple linear regression.
par(mfrow = c(2, 2))
plot(res)
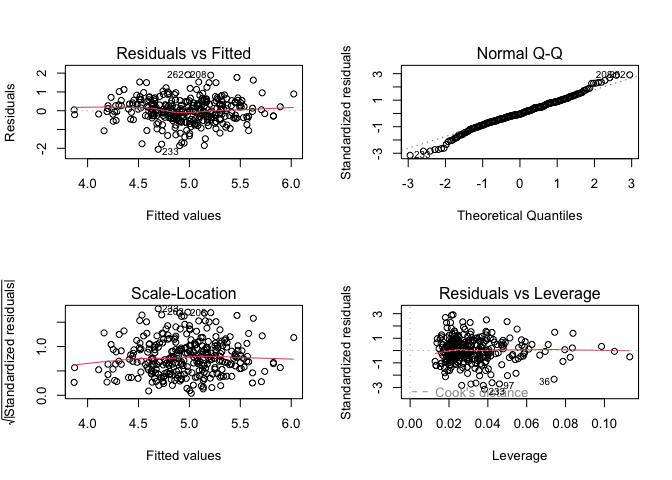
Key Points
Multiple linear regression is an intuitive extension of simple linear regression.
Transforming your data can give you a better fit.
Check for outliers, but ensure you take the correct course of action upon finding one.